Атом во внешнем поле. Эффекты Зеемана и Штарка

Лекция 4.

АТОМ ВО ВНЕШНЕМ ПОЛЕ. ЭФФЕКТЫ ЗЕЕМАНА И ШТАРКА.

При помещении атома во внешнее магнитное или электрическое поле его симметрия изменяется – появляется выделенная ось симметрии, направленная вдоль напряженности внешнего поля. Это приводит к изменению внутренней энергии атома за счет взаимодействия орбитального и полного магнитного момента атома с внешним полем, энергия которого определяется проекциями этих моментов на направление вектора напряженности поля. Ранее вырожденные по квантовому числу m_l энергетические уровни расщепляются. Величина расщепления определяется напряженностью внешнего поля. В свою очередь, расщепление уровней приводит к тонкому расщеплению спектральных линий.

Эффект Зеемана. Он проявляется в расщеплении спектральных линий, излучаемых атомами, помещенными во внешнее магнитное поле. Суть этого эффекта достаточно просто объясняется взаимодействием магнитного момента атома с внешним полем. Рассмотрим простейший случай взаимодействия орбитального магнитного момента одного электрона, находящегося в состоянии, описываемом квантовыми числами nl. Напомню, магнитный орбитальный момент электрона связан с механическим орбитальным моментом через магнитон Бора m₀ соотношением:

,                                         (1)

где 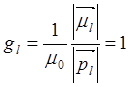- гиромагнитное соотношение для орбитального движения. Взаимодействие этого момента с внешнем полем напряженностью  приводит к появлению добавочной энергии:

.            (2)

Напомню, что квантовое число m_l, квантующее проекцию орбитального момента количества движения, может принимать 2l+1 значение – от –l через единицу до +l. Поэтому во внешнем магнитном поле энергетический уровень атома, определяемый квантовыми числами n и l, расщепляется на 2l+1 компонентов. Величина расщепления определяется абсолютной величиной напряженности магнитного поля и проекцией орбитального момента на его направление, но не зависит от самих квантовых чисел n и l. В системе этих расщепленных уровней разрешаются оптические переходы либо без изменения m_l (Dm_l =0), либо при его изменении на единицу (Dm_l =±1). В первом случае излучение оказывается линейно поляризованным в направлении, перпендикулярном направлению поля. Эта компонента называется p-компонентой. Во втором случае спектральные линии (s-компоненты) имеют круговую поляризацию при наблюдении вдоль направления поля. Т.е. в спектре вместо одной линии проявляются три компоненты, между которыми частотное расстояние одинаково и равно:

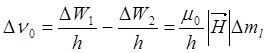.                       (3)

Такой эффект называется нормальным эффектом Зеемана. Мы его обосновали без учета спинового магнитного момента. Поэтому нормальный эффект проявляется у атомов на переходах между синглетными уровнями, у которых скомпенсированы спиновые моменты S=0, или на переходах между уровнями, у которых L>>S. Учет спинового момента усложняет картину расщепления. В зависимости от напряженности магнитного поля наблюдается два типа расщепления энергетических уровней. Один тип характерен для слабого поля, при котором магнитное расщепление меньше мультиплетного, а второй для сильного поля, при котором магнитное расщепление больше мультиплетного.

Учтем спиновый магнитный момент электрона в атоме, для которого выполняется приближение LS-связи. В этом приближении полный магнитный момент атома образуется в результате векторного сложения суммарного орбитального и суммарного спинового магнитных моментов. Причем направления полных магнитных и механических моментов, в общем случае, не совпадает. Это обусловлено тем, что гиромагнитное отношение для спина g_s =2, а для орбитального момента g_s =1.

В случае слабого магнитного поля полный магнитный момент атома быстро прецессирует вокруг полного механического момента и с меньшей скоростью – вокруг направления магнитного поля. Полный магнитный момент можно разложить на две составляющие, одна из которых параллельна (m_II), а вторая перпендикулярна (m_^) механическому моменту. Из-за большой скорости прецессии среднее по времени значение перпендикулярной составляющей равно нулю, а параллельной составляющей равно

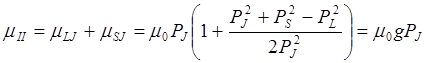.           (4)

Здесь g, равная величине в скобках, называется множителем Ланде. Учитывая (4) получает энергетическое расщепление уровней в слабых полях

,                                  (5)

которое отличается от (2) наличием множителя Ланде и заменой квантового числа m_l для одного электрона на квантовое число M_J, квантующее проекцию полного механического момента всего атома. Т.е. в слабых магнитных полях происходит расщепление уровня с квантовым числом J на 2J+1 подуровень – вырождение полностью снимается. При этом величина расщепления через множитель Ланде зависит от квантовых чисел L, S и J, но не зависит от главного квантового числа n.

В результате расщепления энергетических уровней происходит расщепление спектральных линий на линейно поляризованные p-компоненты – при DM_J =0, и поляризованные по кругу s- компоненты – при DM_J =±1. При этом переход с M_J1 =0 на M_J2 =0 запрещен. Частотный интервал между компонентами равен

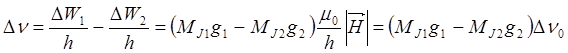.         (5)

Здесь разность в скобках есть правильная дробь, а Dn₀ – рассмотренное выше без учета спина нормальное расщепление.