Атом во внешнем поле. Эффекты Зеемана и Штарка, страница 4

.                                       (12)

То есть квадратичный эффект переходит в линейный (рис. 4). Такая зависимость характерна при учете взаимодействия только двух уровней. Однако с увеличением напряженности электрического поля все большую роль начинают играть члены, учитывающие взаимодействие с другими уровнями. Вследствие этого зависимость от E становится не линейной, а более сложной.

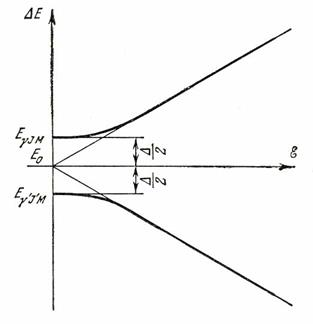
Рис.4. Переход квадратичного Штарк-эффекта в линейный.

Расщепление спектральных линий, как и для атома водорода, обусловлено правилами отбора: M®M – p-компонента, M®M±1 - s-компоненты. Частоты p и s-компонент определяются соотношениями:

,

,                       (13)

Величина расщепления сильно падает с увеличением D - разности энергий между уровнями, поэтому, как правило, расщепление линий целиком определяется расщеплением верхнего терма. При максимальной напряженности электрического поля в газе E=10⁵ В/см, не вызывающей его пробой, величина расщепления имеет порядок 1 см^-1 при D=10 см^-1. Но в случае молекул и конденсированных сред, в которых собственные внутренние электрические поля имею гораздо большие значения – порядка 10⁸ В/см – штарковское расщепление достигает большой величины в несколько электроновольт.

В заключение следует отметить, что в переменном стохастическом электрическом поле, которое реализуется в плазме газового разряда, Штарк-эффект проявляется в виде уширения уровня и, соответственно, штарковского уширения спектральных линий. Это еще один сильный механизм уширения спектральных линий. Поскольку в плазме газового разряда стохастические электрические поля формируются главным образом свободными электронами, как наиболее быстрыми заряженными частицами, то по штарковскому уширению линий можно определять концентрацию электронов в плазме. Для этого обычно используют спектральные линии водорода, как наиболее чувствительные к этому эффекту. К тому же атомы водорода, как самые малые атомы, легко проникают через любые стенки. Поэтому в земных условиях в любой плазме присутствуют атомы водорода.

Литература.

М.А. Ельяшевич. Атомная и молекулярная спектроскопия. М.: Гос.изд-во физ.-мат. лит-ры, 1962, 892 с.

И.И. Собельман. Введение в теорию атомных спектров. М.: Гос.изд-во физ.-мат. лит-ры, 1963, 640 с.

С.Я. Фриш. Оптические спектры атомов. М.: Гос.изд-во физ.-мат. лит-ры, 1962, 792 с.

Лекция 4.

АТОМ ВО ВНЕШНЕМ ПОЛЕ. ЭФФЕКТЫ ЗЕЕМАНА И ШТАРКА.

Эффект Зеемана

,                                         (1)

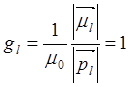 – гиромагнитное соотношение для орбитального движения.            .            (2)

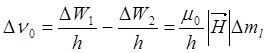.                       (3)

Dm_l =0 – p-компонента, Dm_l =±1 – s-компонента.

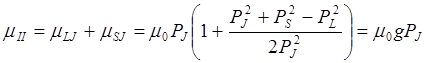.           (4)

g – множитель Ланде.

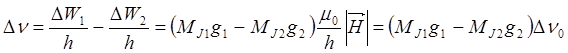,                                  (5)

.         (5)

DM_J =0 – p-компонента, DM_J =±1 – s- компонента. С M_J1 =0 на M_J2 =0 запрещен.

,                                           (6)

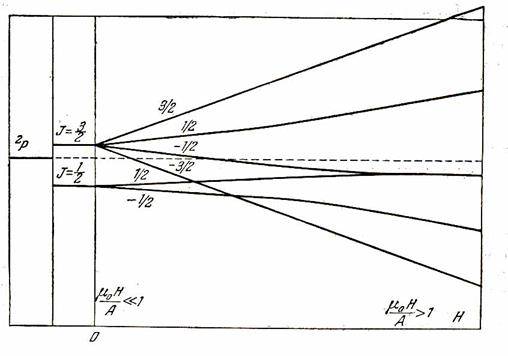
Рис.1. Расщепление термов ²P в слабом и сильном магнитных полях.

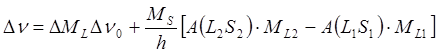.                   (7)

DM_S = 0, DM_J =0 – p-компонента, DM_J =±1 – s- компонента.

Эффект Штарка

,                                                 (8)

 - дипольный момент атома, не равный нулю, если связывающие состояния атома разной четности .

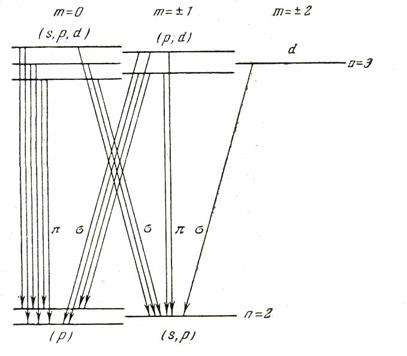
Рис.2. Расщепление уровней водорода n=2,3 в электрическом поле.

Dm=0 – p-компоненты, Dm= ±1 – s-компоненты.

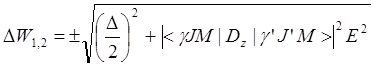.                     (9)

gJM – уровень 1 и g’J’M – уровень 2.

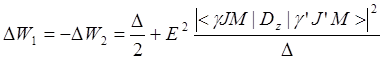.                 (10)

.                                                    (11)

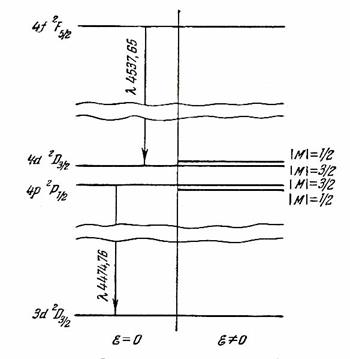
Рис.3. Расщепление линий l=453,765 и 447,476 нм ArII в электрическом поле.

.                                       (12)

Рис.4. Переход квадратичного Штарк-эффекта в линейный.

,

,                       (13)