При помещении атома водорода или водородоподобных ионов в электрическое поле каждый уровень, характеризуемый главным квантовым числом n, расщепляется на 2n-1 компонент, характеризуемые положительными значениями магнитного квантового числа m=0, 1,2,…(n-1). Величина этого расщепления пропорциональна абсолютной величине напряженности электрического поля, и она одинакова для всех компонент уровня n. Оптические переходы между компонентами уровней n и n±1 возможны при неизменном m (Dm=0) или при его изменении на единицу (Dm= ±1). Как и в случае магнитного поля при переходах при Dm=0 перпендикулярно направлению электрического поля наблюдаются линейно поляризованные p-компоненты, а при Dm= ±1 – поляризованные по кругу s-компоненты. В отличие от эффекта Зеемана для эффекта Штарка характерно наличие значительно большего числа и p и s-компонент. Например, при переходах между уровнями с n=3 и n=2 атома водорода, помещенного в постоянное электрическое поле проявляются восемь p и восемь s-компонент (рис.2).
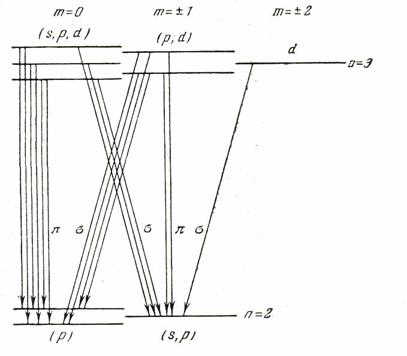
Рис.2. Расщепление уровней водорода n=2,3 в электрическом поле.
Линейный эффект Штарка достаточно просто регистрируется при напряженности внешнего электрического поля порядка E=105 В/см. Эта величина близка к критической напряженности, при которой происходит пробой газового промежутка.
Для остальных атомов линейный эффект Штарка такого типа не наблюдается, но всегда имеет место квадратичный эффект Штарка, который обусловлен совместным взаимодействием энергетических состояний атома, характеризуемых квантовыми числами gJM (уровень 1) и g’J’M (уровень 2) друг с другом и с внешним электрическим полем. Такой учет дает выражение для изменения энергетического расстояния между этими уровнями под действием внешнего электрического поля в виде выражения:
.
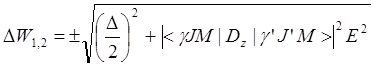(9)
Здесь DZ – проекция дипольного момента на направление электрического поля E, D - энергетическое расстояние между уровнями в отсутствии электрического поля. Выражение (9) справедливо тогда, когда D много меньше разности энергий между рассматриваемыми уровнями и любыми другими уровнями атома. В случае слабого электрического поля, т.е. поля, добавка энергии от которого (второй член под корнем) много меньше (D/2)2 (первый член под корнем), то разложение корня (9) в ряд дает формулу квадратичного Штарк-эффекта:
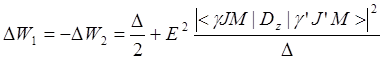. (10)
в этой формуле второй член и является дополнительной энергией, получаемой атомом от поля и вызывающим расщепление энергетического уровня по проекциям полного момента атома на ось z, совпадающей с направлением электрического поля. Зависимость матричных элементов Dz от квантового числа M вычисляется в явном виде. После вычислений добавку энергии от взаимодействия атома с электрическим полем можно записать в простом виде:
.
(11)
Это выражение прямо указывает на
то, что энергетический уровень gJ расщепляется на компоненты 
(рис.3),
причем величина расщепления пропорциональна квадрату напряженности
электрического поля.
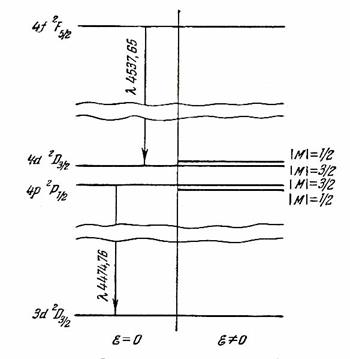
Рис.3. Расщепление линий l=453,765 и 447,476 нм ArII в электрическом поле.
Все уровни, за исключением уровня M=0, двукратно вырождены по знаку проекции момента. Уровни J=0 и J=1/2 не расщепляются, а только испытывают сдвиг. Характерной особенностью этого Штарк-эффекта является асимметрия расщепления – сильная зависимость расщепления от M. Несмотря на простоту выражения (11), сам процесс вычисления добавки энергии уровня в электрическом поле представляет собой сложную задачу вычисления коэффициентов AgJ и BgJ .
В случае сильного поля, когда второй член под корнем выражения (9) много больше первого, добавку энергии от поля можно представить в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.