















|
Лекция |
11 |
|
ДЛИННЫЕ ЛИНИИ С НЕЛИНЕЙНЫМИ ПАРАМЕТРАМИ |
|
§ 23.1 Введение
При изучении распространения электромагнитных волн в линиях, как известно, используют телеграфные уравнения (см. главу 2). Они получаются путем упрощения уравнений Максвелла. В общем виде они не содержат в себе никаких предположений относительно пространства, в котором распространяется волна, и линейны относительно входящих в них физических величин – полей, индукций и тока проводимости. Для отыскания решений системы уравнений Максвелла необходимо конкретизировать свойства пространства, в котором распространяется волна. Из всего многообразия свойств обычно указываются его геометрия и связь индукций и тока проводимости с полями, характеризующая среду, заполняющую это пространство. Если пространство безграничное, то указывается, какие источники возбуждают волну. В ограниченном пространстве, не содержащем источников, указывается, какие волны приходят («падают») извне на его границу и свойства граничащего пространства. В том и другом случае необходимо знать состояние среды и поля в ней до воздействия волны.
Электрические и магнитные свойства пространства зависят, как известно, от термодинамического состояния заполняющей его среды. Например, значительное изменение температуры вызывает изменение связи индукций и тока проводимости с полями. Поэтому в общем случае система уравнений, описывающая распространение волн и состоящая из уравнений Максвелла, уравнений связи, характеризующих среду, и уравнений термодинамики, является системой, содержащей нелинейные уравнения. В данной главе мы ограничимся случаем, когда электромагнитные волны не меняют термодинамического состояния среды, не вызывают ее электрических пробоев или частичной ионизации. При этом распространение волн описывается системой уравнений Максвелла.
Как известно, среду, заполняющую пространство, можно характеризовать такими параметрами, как проницаемость и проводимость. Они являются коэффициентами пропорциональности в линейных уравнениях связи индукций и тока проводимости с полями. Функциональный вид уравнений связи имеет место при не слишком быстрых изменениях полей. При быстрых изменениях полей ток проводимости и индукции изменяются с запаздыванием. Это запаздывание можно охарактеризовать промежутком времени, в течение которого среда приходит к равновесию после скачкообразного изменения полей.
Обычно рассматривались волны в таких средах, параметры которых можно считать постоянными. В результате была создана теория электромагнетизма, в основе которой лежат линейные уравнения. Очевидно, если любая из четырех величин является функцией напряженности хотя бы одного поля волны, то система уравнений Максвелла становится нелинейной. Многие интересные явления могут быть рассмотрены только в рамках теории, основанной на нелинейных уравнениях. К числу таких явлений относятся ударные электромагнитные волны.
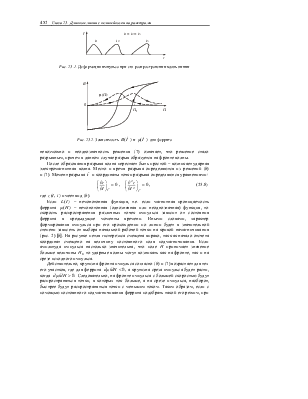
Термин «ударные волны» впервые был использован в газодинамике в конце XIX в. при изучении нелинейного течения газов. Из акустики известно, что квадрат скорости распространения звуковой волны равен производной по плотности среды от давления и является локальным свойством среды. Связь между давлением и плотностью (калорическое уравнение состояния) является нелинейной. Например, для воздуха при умеренных температурах давление пропорционально плотности в степени 1,4. Следовательно, скорость звуковой волны в воздухе зависит от его плотности. В акустике, как правило, рассматриваются слабые возмущения, амплитуда волны давления весьма незначительна, поэтому нелинейность уравнения состояния не учитывается. Уравнения газодинамики, нелинейные в общем случае, для малых возмущений линеаризуются. Сильные возмущения приводят к нелинейным течениям газа. Смысл производной по плотности от давления при нелинейном течении газа сохраняется, но это локальное свойство среды зависит от точки на профиле распространяющейся волны. В акустическом приближении форма звуковой волны при распространении остается неизменной. Однако для сильной волны, например волны сжатия, скорость распространения вершины профиля волны больше, чем основания. Следовательно, происходит деформация профиля волны, так же, как при набеге морской волны на берег: фронт (передняя сторона) профиля становится круче, спад положе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.