Длинные линии с нелинейными параметрами, страница 5

Теория ударных электромагнитных волн подробно освещена в работе [1]. Далее мы остановимся лишь на некоторых выводах из этой теории, необходимых для практических расчетов.

Для описания процессов в линиях передачи с нелинейными параметрами авторы работы [8] воспользовались телеграфными уравнениями для однородной линии в сочетании с уравнением (22.4) для учета диссипативных свойств феррита. Ими была найдена величина длительности фронта стационарной ударной волны в линии передачи с ферритом:

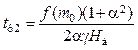,                                              (23.9)

где  ( – начальная намагниченность феррита). О величинах  и  сказано в § 22.1. График функции  приведен на рис. 5. При анализе распространения стационарной волны вдоль линии можно ввести понятия эффективной магнитной проницаемости феррита для ударного фронта:

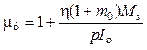                                           (23.10)

и сопротивления линии ударной стационарной волне:

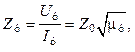                                             (23.11)

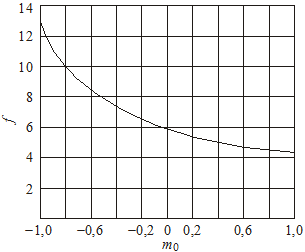
Рис. 23.5. График функции  f (m₀)

где  ( и  – погонные индуктивность и емкость линии);  – коэффициент заполнения, зависящий от геометрии поперечного сечения линии и феррита;  – коэффициент, зависящий от конфигурации линии передачи.

Полученное для линии с распределенными параметрами выражение (10) справедливо для линии с сосредоточенными параметрами лишь в том случае, если можно пренебречь дисперсией, связанной с дискретностью параметров линии,

                                              (23.12)

В реальных нелинейных линиях с сосредоточенными параметрами длительность фронта стационарной ударной волны совпадает с постоянной времени ячейки для ударной волны [9]:

                                              (23.13)

В [7] найдено расстояние  при котором амплитуда разрыва достигает максимального значения, т.е. то расстояние, которое должна пройти волна по нелинейной линии до момента образования стационарной ударной волны.

Для линии с сосредоточенными параметрами оптимальным является следующее количество ячеек в линии:

.                                          (23.14)

Любой генератор мощных наносекундных импульсов на линиях с ферритом представляет собой волновую систему, одна часть которой выполнена в виде однородных отрезков линий с ферритом, другая – в виде линейных линий передачи. При этом необходимо согласование элементов системы для обеспечения максимальной передачи мощности в нагрузку и получения импульсов заданной формы. В том случае, если линия имеет согласованную нагрузку, условием формирования импульсов правильной формы и полной передачи мощности в нагрузку является равенство выходного сопротивления линии с ферритом  при полном насыщении феррита и неизменном направлении вектора намагниченности сопротивлению нагрузки [10]:

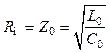.                                               (23.15)

Если исходный импульс поступает в линию с ферритом через линейную линию с волновым сопротивлением  то для полной передачи мощности необходимо согласование сопротивления  и сопротивления нелинейной линии ударной волне:

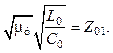                                               (23.16)

Очевидно, что длина линии с ферритом должна быть такова, чтобы после прохождения по ней фронт исходного импульса ликвидировался полностью, а длительность вершины не менялась. При этом для передачи видеоимпульса без искажений (за исключением переднего фронта) необходимо выполнение следующего условия для длительности вершины исходного импульса [10]:

,                                                    (23.17)

где  – длина линии с ферритом,  – скорость волны в линии с насыщенным ферритом.