Длинные линии с нелинейными параметрами, страница 3

где  – напряжение между проводами в сечении z (двухпроводная линия);  – ток в одном из проводов в том же сечении;  – заряд на единицу длины линии;  – поток индукции на единицу длины линии. Для достаточно медленных процессов поток  считается только функцией тока:

                                                       (23.3)

Заряд  линейно связан с напряжением:

                                                        (23.4)

где  – емкость на единицу длины линии.

Уравнения (2) пригодны для случая неоднородных и искусственных линий, если величины, входящие в эти уравнения, заменить их средними значениями, при условии, что временные и пространственные масштабы  и  намного больше соответствующих масштабов отдельного звена линии.

Нелинейные уравнения (2)–(4) в общем случае не решены. Однако известны их частные решения для случая так называемых простых волн, когда одна из искомых величин является однозначной функцией другой величины. Полагая U = U(I), можно найти:

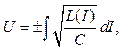                                                (23.5)

тогда уравнения (2) будут иметь решения, записанные в виде [6]:

                                                (23.6)

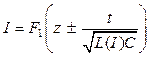,                                             (23.7)

где  и  – произвольные функции, определяемые из граничных и начальных условий,  – индуктивность на единицу длины линии, v - скорость волны в линии.

Решение (6) имеет вид бегущей волны (простая волна). У простой волны каждая точка ее фронта движется со скоростью, зависящей от значения тока в этой точке. Если индуктивность  линии является монотонно убывающей функцией абсолютной величины тока, то с большей скоростью будут распространяться те точки фронта, где ток больше. Следовательно, в случае передачи импульса крутизна его фронта вдоль линии возрастает, а срез импульса становится более пологим (рис. 1). Решение (7) допускает, что в некоторые моменты времени отдельные точки на фронте волны «обгонят» точки с меньшим значением тока. Решение (7) при этом становится неоднозначным (при  на рис. 1). В действительности это

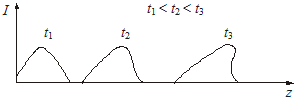
Рис. 23.1. Деформация импульса при его распространении вдоль линии

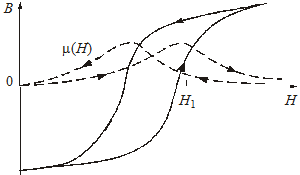
Рис. 23.2. Зависимость  и  для феррита невозможно и неоднозначность решения (7) означает, что решение стало разрывным, причем в данном случае разрыв образуется на фронте волны.

После образования разрыва волна перестает быть простой – возникает ударная электромагнитная волна. Место и время разрыва определяются из решений (6) и (7). Момент разрыва  и координаты точки разрыва определяются уравнениями:

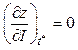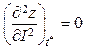,    ,                                        (23.8)

где  имеет вид (6).

Если  – немонотонная функция, т.е. если магнитная проницаемость феррита  – немонотонная (однозначная или неоднозначная) функция, то скорость распространения различных точек импульса зависит от состояния феррита в предыдущие моменты времени. Иными словами, характер формирования импульса при его прохождении по линии будет в значительной степени зависеть от выбора начальной рабочей точки на кривой намагничивания (рис. 2) [6]. На рисунке петля гистерезиса смещена вправо, так как начало отсчета координат смещено на величину постоянного поля подмагничивания. Если амплитуда импульса настолько значительна, что поле Н принимает значение больше величины Н₁, то ударные волны могут возникать как на фронте, так и на срезе исходного импульса.

Действительно, крутизна фронта импульса согласно (6) и (7) возрастает для тех его участков, где для феррита  а крутизна среза импульса будет расти, когда  Следовательно, на фронте импульса с большей скоростью будут распространяться точки, в которых ток больше, а на срезе импульса, наоборот, быстрее будут распространяться точки с меньшим током. Таким образом, если с помощью постоянного подмагничивания феррита подобрать такой его режим, при котором зависимость магнитной проницаемости от напряженности будет иметь максимум, то получим волну с крутым фронтом и срезом (рис. 3).