Проблемы создания медицинских систем и комплексов, страница 9

Постулат об идеальности свойств сократительного элемента позволяет определить V₀(t) из эксперимента как скорость сокращения мышцы при изотоническом сокращении с пулевой постнагрузкой (F(t) = F_н =const), а также определить значение С, а точнее, характеристику жесткости последовательного элемента:

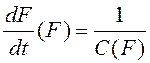.                                              (2.21)

Эта характеристика получается, если продифференцировать кривую «сила – длина» (F – l) из работы по l и затем перестроить производную по переменной F, используя саму кривую F(t) (рис. 2.8, а). Адекватная аппроксимация кривой имеет вид:

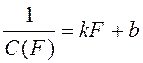,                                               (2.22)

где (k = 0,5^{–1 мм,}b = 1,4 г/мм).

Хорошую аппроксимацию функции скорости сократительного элемента дает функция V₀(t) =At²e^–ª¹. Об адекватности модели и справедливости постулата можно судить, сравнив экспериментальные кривые и  (сплошная линия) с расчетными кривыми 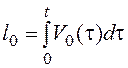 (штриховая линия) на рисунке 2.8 (б), построенными по экспериментальной кривой изометрического усилия F_пз(t)путем подбора наилучших значений параметров к и b. При этом использовалась формула: 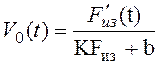 (k = 0,3 мм^–1, b = 2,5 г/мм), полученная из уравнений модели (2.18), (2.19).

Двухэлементная модель адекватно описывает более узкий, чем четырехэлементная, круг экспериментальных данных: усилия изометрического сокращения, длины укорочения при изотонических сокращениях при разных постнагрузках и скорость при нулевой постнагрузке. Следует заметить, что для оценки сократительных свойств сердечной мышцы в организме этого достаточно, так как быстрые деформации (порядка миллисекунд) соответствуют отсутствию мышц в сердце. Зато рассматривается модель значительно проще, в ней существенно меньше свободных параметров, определяющих сократительные свойства: к, b, А, а, F_а.

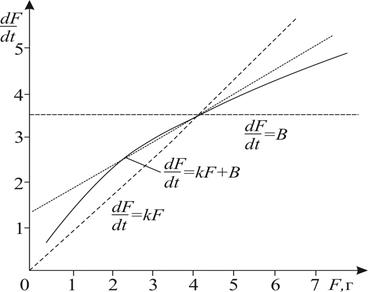
Рис. 2.8. Характеристика жесткости последовательного элемента в двухэлементной модели мышцы

Это позволяет использовать ее в практических задачах скрининга фармакологических препаратов путем оценки (идентификации) параметров по экспериментальным кривым изометрического усилия и изотонической длины (или скорости укорочения), что даст возможность сравнивать эффективность препаратов в их воздействии на сократительный  аппарат мышцы.

Из описанной двухэлементной модели вытекает строгое обоснование двух изоволюмических индексов сократимости, довольно широко используемых в эксперименте и в кардиохирургии:

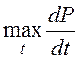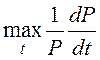;                               , где Р – внутрижелудочковое давление как функция времени в течение изоволюмической фазы сокращения. Для такого обоснования надо считать, что механика целостного желудочка тождественна механике изолированной мышцы (ниже будет показано, что это не совсем так), и использовать две другие, более простые аппроксимации характеристики жесткости (рис. 2.8):

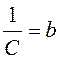,(b=3.5 г/мм);  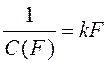            , (k=0.85 мм^-1).

Таким образом, индексы рассчитываются как максимальные значения скорости сократительного элемента при изоволюмическом сокращении. Эти величины равны максимальной скорости сократительного элемента при изотоническом сокращении с нулевой постнагрузкой вследствие его идеальности, что и служит оценкой его сократительных свойств. Следует заметить, что обоснование этих индексов, традиционно проводимое многими авторами (начиная с Зонненблика) на основе модели Хилла, в которой сократительный элемент не наделяется идеальными свойствами, не является строгим.

Обратим внимание также на то, что многие физиологи и клиницисты приписывают одному из этих или подобных им индексов способность отразить исчерпывающим образом сократительные свойства сердца в качестве универсального скалярного показателя. Однако, как было показано выше, даже довольно простая двухэлементная модель имеет пять параметров. Поэтому возникает вопрос о простейшей модели с минимальным числом параметров, еще пригодной для оценки сократительных свойств.