Оценка сократительных свойств заключается в оценке параметров уравнения (2.13) или системы (2.15, 2.16). Однако специфика этой задачи состоит в том, что возмущение ип(t) и его производные, как правило, непосредственно не измеряются, поэтому возникает необходимость в параметризации функции и0(t), и в задачу оценки сократительных свойств входит также оценка этих параметров по измерениям z и и. Как отмечалось выше, экспериментальные и клинические данные, по которым производится оценка параметров модели, страдают неполнотой и низким качеством, поэтому модели должны быть, по возможности простыми. Однако степень полноты и качественности данных в различных применениях все же неодинаковы. Поэтому приходится разрабатывать одновременно несколько моделей одного и того же объема, но различной сложности, для разных применений.
Ниже будут описаны три математические модели изолированной сердечной мышцы, расположенные в порядке убывающей сложности.
Четырехэлементная модель. Она состоит из четырех элементов: активного АЕ – идеального источника скорости укорочения (кинетической переменной) V0(t), не зависящей от усилия F (потенциальной переменной), получающегося при укорочении мышцы с нагрузкой, и трех пассивных элементов: двух эластичностей С1, и С2 и вязкости R (рис. 2.7).
Система дифференциальных, описывающая процесс сокращения мышцы, имеет вид:
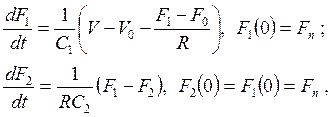(2.17)
где V – скорость укорочения мышцы, F1=F – общее усилие мышцы, F2 – усилие на эластичности С2. Модель нелинейна: эластичность и вязкость зависят от переменной F:
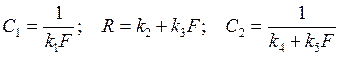(2.18)
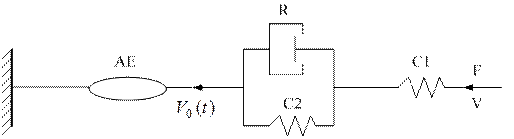
Рис. 2.7 – Структурная схема механики четырехэлементной модели сердечной мышцы
Эта модель может быть описана также одним уравнением типа (2.13):
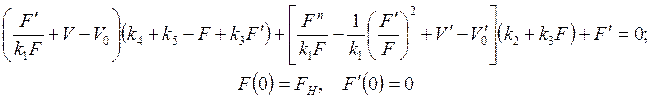(2.19)
Параметризация функции скорости активного элемента проведена в виде:
.
Сократительные свойства мышцы определяются значениями свободных параметров к1 – к3, a1 – а3, F. Выбор их значений надлежащим образом позволяет достаточно адекватно описать поведение мышцы практически во всех видах экспериментов по изучению механики сердечной мышцы, проводимых в настоящее время: изометрическое и изотоническое сокращение с различными пред- и постнагрузками, опыты быстрого растяжения и высвобождения, инактивацию деформацией и др. Вид и соотношение кривых «сила – скорость», построенных всеми известными в настоящее время способами по данным модели, идентичны построенным по экспериментальным данным. То же относится и ко всем известным способам построения кривых активного состояния.
Выбор следующих значений параметров обеспечивает адекватность модели экспериментальным данным: k1= 4,5 мм–1; k2 = 0,04 г×с×мм–1; k3 = 0,2 с×мм–1; k4 = 1,2 г×мм–1; k5 = 0,5 мм–1 при V≥0. При V<0 выбираются другие значения: k2 = 0,2 г×с×мм–1; k3 = 0; k4 = 0,83г×мм–1; k5 = 0,5 мм–1. Кроме того, а1 = 155 мм×с–2; а2 = 0,7 с–1; a3 = 1 мм×с–1; Fн= 0,5 г.
Однако для целей практического применения четырехэлементная модель оказывается чересчур усложненной, имеет слишком много свободных параметров. Поэтому была разработана более простая, двухэлементная модель.
Двухэлементная модель изолированной сердечной мышцы. Структурная схема механики данной модели полностью тождественна схеме модели Хилла: сократительный (активный) элемент и последовательно соединенный пассивный эластичный элемент. Однако между этими моделями имеется существенное различие. Оно заключается в том, что сократительный элемент наделен свойствами идеального источника скорости (укорочения). Это позволило записать дифференциальное уравнение модели в виде:
, (2.20)
где V – скорость укорочения мышцы, F' – производная по времени от усилия, С – эластичность последовательного пассивного элемента, V0 = V0(t) – скорость укорочения сократительного элемента, зависящая только от времени и не зависящая от усилия F.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.