Проблемы создания медицинских систем и комплексов, страница 3

2.1. Физиологические системы организма как компонент БТС

Если в БТС эргатического типа в качестве биологического компонента включаются системы кибернетического комплекса организма, то в инженерно-физиологических системах организм представлен своей метаболической частью. Задача технического компонента БТС во втором случае состоит в обеспечении нормального функционирования биохимической (метаболической) системы организма (рис. 2.3, б).

Динамические свойства метаболической системы организма в первую очередь определяются скоростями протекания в ней основных биохимических процессов (синтез биополимеров, формация макромолекул, сборка внутриклеточных структур). Непрерывное бесперебойное протекание этих процессов обеспечивается физиологическим комплексом организма. Физиологические системы образуют потоки веществ и энергии, направленные от физиологических «источников» к биохимическим «стокам». Потоки веществ – субстратов, топлива, окислителя – но пути от источников к стокам образуют один или несколько компартментов. (Под компартментом здесь, как и обычно, понимается некоторое количество вещества, которое обособлено в том смысле, что в процессах транспорта или обмена его можно рассматривать как единое целое.) Одновременно в системе протекают и противоположно направленные процессы – катаболизм, т. е. разложение сложных отходов жизнедеятельности на простые вещества. При этом порождаются (также идущие от биохимических центров – источников – к физиологическим стокам) потоки тепла и деградированных веществ.

Процессы в биохимической системе определяют скорости процессов в физиологических источниках. Поэтому будем говорить, что биохимические процессы задают потребности, формально описываемые как скорости (темпы) необходимых потоков подведения расходуемых или отведения образующихся веществ. Опишем эти потребности вектором[3]:

,                                                   (2.1)

где ,  – темпы потоков, отвечающие основному обмену организма.

Физиологический комплекс формирует совокупность N потоков:

y=[y₁,y₂,...,y_n]Т,                                                                 (2.2)

где N > п, в норме уравновешивающую совокупность потоков . Пусть рассматривается m компартментов x_i, i = 1,2,…,m:

x = [x₁, x₂,. . .,x_m]Т.                                                            (2.3)

Тогда для каждого из них можно написать уравнение баланса масс:

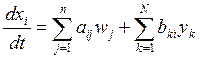,                                                         (2.4)

где все коэффициенты равны 0 или ± 1, что отражает связи i-го компартмента с другими компартмептами (b_ij), а также с источниками и стоками (а_ij).

Формулы (2.1) – (2.4) описывают метаболическую систему в терминах пространства состояний современной теории управления. Вектор х – вектор состояния,  – задающий вход.

Не специфические переменные, характерные для физиологических процессов регуляции в организме (давления, кровотоки, частота сердечных сокращений и т. д.), являются теперь алгебраическими функциями координат вектора х. Если обозначить все эти переменные символами u_i:

и = [u₁, u₂,…,u_r]т,                                                            (2.5)

то можно сказать, что вместе с совокупностью потоков у, они образуют вектор выхода системы z:

z = [y₁,y₂,…y_n; u₁,u₂,…,u_r]т,                                            (2.6)

Введем еще вектор внешних условий v:

v = [v_1,v₂,…,v_i]т.                                                               (2.7)

Тогда можно написать:

u_i =f_i(y,v).                                                                          (2.8)

Вектор и описывает собственные активные механизмы управления физиологическоим комплексом организма. Эти механизмы регулируют потоки у_к в соответствии с метаболическими потребностями организма:

y_k = f_k(u) = F_k (x,v),                                                           (2.9)