Простейшая модель сердечной мышцы. Векторная концепция сократимости. Эта модель представляет собой упрощенный вариант двухэлементной модели, описанной выше: идеальный сократительный элемент со скоростью V0(t) и последовательный упругий элемент с постоянной эластичностью С (простейшая аппроксимация жесткости упругого элемента).
Дифференциальное уравнение имеет вид:
CF’+V–V0=0, F(0)=Fн. (2.23)
Проинтегрировав это уравнение, по времени получим алгебраическое уравнение:
С(F–Fн)+l - l0=0, (2.24)
где 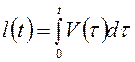 ,
, 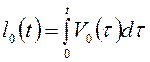 – длины
укорочения мышцы и сократительного элемента соответственно.
– длины
укорочения мышцы и сократительного элемента соответственно.
Простейшей параметризацией функции сократительного элемента является использование величин: Vm= mах V0(t) – в первом случае и 1т = mахV0(t) – во втором. В этой модели оценку сократительных свойств мышцы можно произвести, по трем свободным параметрам: Fя, С и Vт или Fя, С и 1т.
Следует заметить, что все три свободных параметра не зависят от постнагрузки как параметра уравнения источника (2.13). Однако еще нельзя считать, что свободные параметры модели оценивают сократительную способность мышцы, так как они зависят от преднагрузки Fн, и она сама входит в число этих параметров. Как показывают результаты ряда работ, значения Vт и lт зависят от преднагрузки хотя и не очень сильно. Что касается эластичности С, то большинство авторов считает, что она зависит от преднагрузки. Однако существует несколько методов экспериментального определения этой величины, и все они дают различные результаты. Наиболее признан в настоящее время метод быстрого высвобождения. Уместно заметить, что упругий элемент, используемый в данной модели, имеет мало общего с упругим элементом, идентифицируемым с помощью упомянутого метода. Жесткость последнего, в 5–10 раз выше, чем используемого в модели. Значение С простейшей модели довольно сильно зависит от преднагрузки.
Следовательно, для оценки сократительной способности необходимо разработать способы нормировки параметров модели на преднагрузку (т. е. приведения их к нормальным значениям Fн). При этом могут возникнуть некоторые трудности, связанные с неаддитивностью начальной длины и изотропных факторов. Для их преодоления придется прибегнуть к двухмерной нормировке как по преднагрузке, так и по изотропным воздействиям.
В результате, мы получим два параметра, оценивающих сократительную способность мышцы: нормированные значения С и Vт или lт. Поскольку эти два параметра являются независимыми и по-разному зависят от преднагрузки, а возможно, и от изотропных воздействий, можно утверждать, что оценку сократительной способности мышцы менее чем по двум компонентам производить нельзя. Другими словами, сократительная способность сердечной мышцы не может считаться скалярным показателем, а является вектором размерности не менее двух.
Следовательно, если ставиться задача моделирования сердечной мышцы, с целью определения оптимальных условий ее работы необходимо моделировать на более высоком уровне, т.е. на уровне желудочка или сердца в целом. Приведенные примеры показывают сложность и многоуровневость управления процессами жизнедеятельности, что приводит к тому, что создание средств замещения или помощи отдельным органам и системам является крайне сложной задачей.
Контрольные вопросы
1. В чем сходство и отличие живых систем от технических?
2. Какая цель моделирования биологических систем?
3. Охарактеризуйте модель сердечной мышцы
4. Возможно ли создание полностью адекватной модели органа или системы живого объекта?
5. Охарактеризуйте двухэлементную модель изолированной сердечной мышцы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.