Статически неопределимая система (СНС). Матричные формулы для вычисления искомых силовых факторов. Расчёт симметричной СНС с использованием разделения на части по оси симметрии

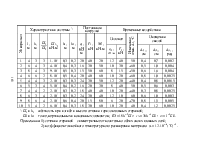
4.КОНТРОЛЬНЫЕВОПРОСЫ

ПОТЕМЕРАСЧЁТНОГОЗАДАНИЯ

1.  Что такое статически неопределимая система (СНС)? ^*)  (3)

2.  Общие свойства статически неопределимых систем  (3).

3.  Что такое степень статической неопределимости (n_st)?  Чему равна n_st?  (4)

4.  По каким формулам можно вычислять n_st для любых плоских стержневых систем?  Для ферм?  (4)

5.  Чем  различаются методы расчёта СНС?  (4)

6.  Что называется основными неизвестными в расчёте СНС? (4)

7.  Идея метода сил  (6).

8.  Что принимается за основные неизвестные в методе сил?  (4)

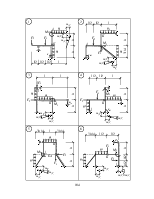
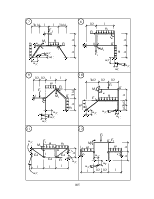
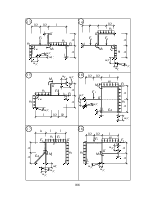
9.  Что такое основная система метода сил (ОСМС)? (6)

Является ли обязательным требование геометрической неизме-няемости ОСМС?  (6, 8)  А статической определимости? (6)

10.  Какую роль играет основная система в расчёте СНС методом сил?  (4, 11)

11.  Сколько различных вариантов ОСМС может быть предложе-но для расчёта некоторой заданной СНС?  (8)

12.  Рекомендации по выбору рационального варианта ОСМС,   их смысл и эффект от их реализации  (8, 9, 11).

13.   Каковы особенности ОСМС при удалении лишних связей:                                               

а) в местах расположения упругих опор?  (7, 8)

б) в местах, где заданы кинематические воздействия (смеще-ния связей)?  (7)

14.  Какие условия (требования) положены в основу вывода уравнений метода сил?  (11)

15.  Каковы по изначальному смыслу канонические уравнения метода сил (КУМС) – статические, кинематические или физи-ческие?  (12)

16.  Варианты записи канонических уравнений метода сил: а) в обычной форме – развернутое и компактное представ-ления  (13);

б) в матричной форме – поэлементная и укрупненная запи- си  (14).

^*)  Здесь и далее в скобках – номера страниц, на которых можно найти ответ на контрольный вопрос. 

17.  Раскрыть смысл:

а) системы КУМС в целом  (13);

б) произвольного (i-го) канонического уравнения  (13);

в) левой части i-го канонического уравнения  (14);

г) свободного члена i-го канонического уравнения D_iS  (D_iF  , D_it , D_ic )  (14);

д) слагаемого d_ik X_k   (14);

е) коэффициента d_ik   (14).

18.  Как называется и какой смысл имеет матрица d  коэффици-ентов КУМС?  (15)

19.  Как использовать матрицу d для проверки геометрической неизменяемости ОСМС?  (16)

20.  Как  называются  и  какой  смысл  имеют  коэффициенты d_ii ?   Коэффициентыd_ik   (14, 15) 

21.  Обозначить на схеме ОСМС и истолковать смысл d_ik (iи k – по заданию) и/или D_iF   (15). 

22.  Свойства компонентов матрицы d  (16).   Теорема о взаимно-сти единичных перемещений в ЛДС (теорема Максвелла)  (14).

23.  Какой должна быть сумма компонентов матрицы d – поло-жительной? Отрицательной? Равной 0?  Любой?  (16) 

24.  Способы определения коэффициентов и свободных членов КУМС  (16).

25.  Формулы для вычисления  d_ik, D_iS , D_iF  , D_it , D_ic :  а) в общем случае  (16) ;

б) для плоской стержневой системы общего вида  (17) ;

в) в частных случаях – для балок, рам, арок, ферм, комби-нированных систем  (см. [ 5 ]).

26.  Матричные выражения для вычисления: а) матриц d, D_S , D_F  , D_t , D_c  (23 – 29);  

б) величин d_ik, D_iS , D_iF  , D_it , D_ic  (cамостоятельно).

27.  Как выполняются универсальная и построчная проверки коэффициентов КУМС?  (18, 19)

28.  Как проверяется правильность вычисления свободных чле-нов КУМС при разных видах воздействий (силовом, темпера-турном, кинематическом)?  (18, 19)

29.  Почему КУМС можно истолковывать как разрешающие уравнения задачи расчёта СНС (синтез статической, кинема-тической и физической сторон задачи)  ( cм. [ 5 ] ).

30.   Как  после вычисления основных неизвестных Х (решения КУМС) определяются искомые силовые факторы в заданной СНС (2 варианта)?  (19, 20)

31.  Особенности вычисления искомых силовых факторов при тем-пературных воздействиях и смещениях связей в случае использо-вания статически определимой основной системы МС  (20, 30).

32.  Матричные формулы для вычисления искомых силовых факторов:      а) в характерных сечениях (расчётных сечениях расчётных участков ОСМС)  (29);       б) в требуемом наборе (в том числе в произвольно назначен-ных сечениях)  (30).

33.  Сколько и каких (перечислить) исходных матриц необходи-мо составить для выполнения расчёта с результатами по вариан-там (а) и (б) предыдущего вопроса?  (30)

34.  Назначение расчётных участков и расчётных сечений эле-ментов с упругими и температурными деформациями при вы-полнении расчёта СНС методом сил в матричной форме (прави-ла, возможности рационального сокращения числа расчётных сечений)  (28).

35.  Из каких частей (блоков) состоят матрицы L₀, B₀ и L_S? (25 – 27)

36.  Как называется каждая из матриц L, B и L_F ?  (25, 26)

37.  Какую структуру (поблочно) и размеры (число строк и стол-бцов) имеют матрицы L, B и L_F ? (25, 26)  Как взаимно согласу-ются размеры и структура этих матриц?  (29) 

38.  Какой смысл имеют компоненты i-го столбца матрицы L ? (23)   f-го столбца матрицы L_F ?  (26)

39.  Вид матриц внутренней упругой податливости расчётных участков с различным числом (3, 2, 1) расчётных сечений  (24).

40.  Какие силовые факторы описываются матрицами L и L_F при расчёте: а) балок, б) рам, в) арок,  г) ферм, д) комбинированных систем?  Как соответственно формируется матрица В?  (самостоятельно)

41.  Как в матрицах L, B и L_F  учитывается наличие в системе упругоподатливых связей?  (23, 24, 26)