г. Новосибирск ММФ НГУ группа 3112
Выполнил: Эльясов А.Б
Проверил: Аверина Т.А
Отчет № 1 по вычислительной практике
Неявный метод Эйлера
(Билет №15)
22.11.2005
План отчета
Постановка задачи
Требуется решить задачу Коши:
(1)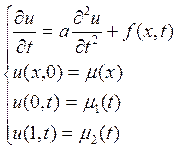 где ,
где ,
![]() используя неявный метод Эйлера, который
выглядит следующим образом:
используя неявный метод Эйлера, который
выглядит следующим образом:
(2)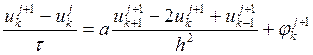
Точное
решение данной задачи с вышеопределенными параметрами: ![]()
Также необходимо:
Метод решения
Неявный метод Эйлера задается системой 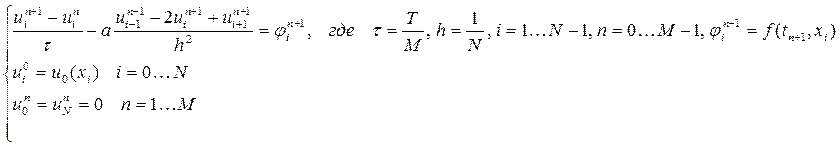 Чтобы решить эту систему, введем
обозначение:
Чтобы решить эту систему, введем
обозначение: 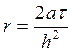 . Тогда получим, что
. Тогда получим, что
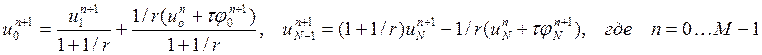 (3) либо
(3) либо
![]() (4)
(4)
При n=0 значения ![]() задаются условиями из
системы. Полагая известными знания
задаются условиями из
системы. Полагая известными знания ![]() , искомыми считают
значения
, искомыми считают
значения ![]() . Тогда совокупность системы с одними из
условий (3) или (4) – это система линейных алгебраических уравнений (сеточных
уравнений) для вычисления
. Тогда совокупность системы с одними из
условий (3) или (4) – это система линейных алгебраических уравнений (сеточных
уравнений) для вычисления ![]() , а решение разностной
задачи сводится к переходу с временного слоя n на временной слой n+1.
, а решение разностной
задачи сводится к переходу с временного слоя n на временной слой n+1.
Для неявной схемы уравнения во внутренних узлах имеют вид
![]() (5)
(5)
где ![]()
Краевые условия могут быть приведены к виду
![]() (6)
(6)
В итоге, для определения вектора ![]() получается система уравнений
получается система уравнений
MU=F (7)
У матрицы М могут быть отличны от нуля лишь
элементы ![]() так что М – трехдиагональная матрица.
Элементы правой части F определяются как
так что М – трехдиагональная матрица.
Элементы правой части F определяются как ![]() .
.
Решение системы (7) вычисляется методом прогонки, суть его в сведении системы уравнений с трехдиагональной матрицей к системе уравнений с двухдиагональной матрицей, т.е в приведении системы к виду
![]() (8)
(8)
Коэффициенты ![]() вычисляются
по рекуррентным формулам
вычисляются
по рекуррентным формулам
![]() (9)
(9)
Начальные значения ![]() вычисляются
из краевых условий (6):
вычисляются
из краевых условий (6): ![]() . Так из условия в
системе получаем, что
. Так из условия в
системе получаем, что
![]() (10)
(10)
а из условий (3)
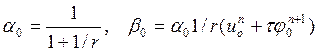 (11)
(11)
Для краевых условий (4), учитывая (5) при j=1, получаем систему уравнений
![]()
Исключая из нее ![]() и преобразуя к виду
и преобразуя к виду ![]() , определим
, определим ![]() .
.
Этап определения коэффициентов прогонки ![]() называют прямой прогонкой, определение
называют прямой прогонкой, определение ![]() , из (8) – обратной прогонкой. Для
осуществления ее необходимо знать
, из (8) – обратной прогонкой. Для
осуществления ее необходимо знать ![]() , которое вычисляется из
краевых условий задачи. Для условий, записанных в системе
, которое вычисляется из
краевых условий задачи. Для условий, записанных в системе ![]() , для условий (3) оно определяется из
системы уравнений
, для условий (3) оно определяется из
системы уравнений
![]() исключением
исключением ![]() :
:
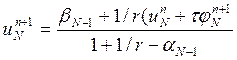 (12)
(12)
При условиях (4) значение ![]() определяется
из системы уравнений
определяется
из системы уравнений
![]() исключением
исключением ![]() ,
, ![]() .
.
Итак, уравнение из системы запишется в таком виде: 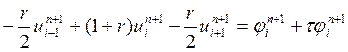 , и есть еще краевые условия
, и есть еще краевые условия ![]() .
.
Исследование порядка аппроксимации схемы и ее устойчивости
Вычислим погрешность аппроксимации и погрешность решения:
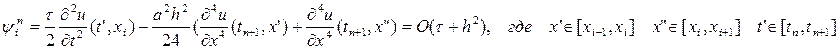
Уравнение для погрешности: 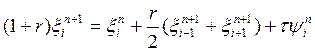 .
Выполним оценку:
.
Выполним оценку:
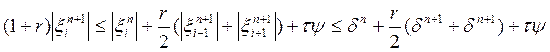 это верно для любого i. Следовательно
:
это верно для любого i. Следовательно
: ![]() . А отсюда, используя то, что
. А отсюда, используя то, что ![]() , получаем
, получаем ![]() .
.
Таким образом, мы получили, что ![]() . То
есть при
. То
есть при ![]() погрешность стремится к нулю со скоростью
погрешность стремится к нулю со скоростью ![]() . Здесь
. Здесь ![]() -
любое.
-
любое.
Таким образом, мы показали, что неявный метод Эйлера безусловно устойчив.
Логическая схема или блок схема программы
Описание тестовых расчетов (тестовые функции, сравнительная таблица расчетов
Анализ результатов и выводы
Список литературы
1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.