Отчет
1. Рассматривается уравнение: y”-2y’-3y=5exp(4x)
Это уравнение переводим в систему: U’=V (1) , где y обозначен через U
V’=2V+3U+5exp(4x)
Известно, решение системы=общее решение однородной сиситемы+частное решение неоднородной сиситемы.
Рассмотрим однородную систему.
| 0 1 |
Матрица системы: А= | 3 2 |
Решаем уравнение |A-λE|=0. Находим корни характеристического уравнения: -1 и 3.
Соответствующие им собственные вектора: (1,-1) и (1,3);
Т.о общее решение однородной системы: z1=c1*(1,-1)*exp(-x)+c2*(1,3)*exp(3x)
Найдем частное решение неоднородной сиситемы:
т.к 4 не является корнем характеристиеского уравнения, будем искать частное решени в виде a*exp(4x). Подставляя его в систему, находим, что a=(1,4).
Итак, общее решение системы:
z= c1*(1,-1)*exp(-x)+c2*(1,3)*exp(3x)+(1,4)*exp(4x)
или
U=c1*exp(-x)+c2*exp(3x)+exp(4x) (2)
V=-c1*exp(-x)+3*c2*exp(3x)+4*exp(4x).
(1) есть аналитическое решение системы.
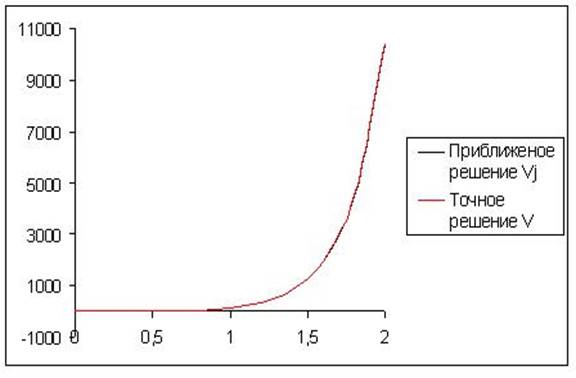
2. Решение задачи Коши для системы (1)
Рассматриваем промежуток x € [0,2].
Начальные условия: U(0)=0; V(0)=0
Аналитическое решение:
система на константы: с1+с2+1=0
-с1+3с2+4=0
Откуда находим с1=0.25; с2=-1.25; затем подставляя данные констант в (2) получим аналитическое решение задачи Коши.
Задача Коши решается методом Рунге-Кутта 4го порядка.
Для системы в общем виде: U’=f(x,U,V)
V’=g(x,U,V)
метод выглыдит следующим образом:
un+1=u n+1/6*h*(k1+2k2+2k3+k4)
vn+1=v n+1/6*h*(q1+2q2+2q3+q4);
где
k1=f(x n, y n, z n); q1=g(x n, y n, z n);
k2=f(x n+0.5h, y n +0.5hk1, z n +0.5hq1); q2=g(x n+0.5h, y n +0.5hk1, z n +0.5hq1);
k3=f(x n+0.5h, y n +0.5hk2, z n +0.5hq2); q3=g(x n+0.5h, y n +0.5hk2, z n +0.5hq2);
k4=f(x n+h, y n +hk3, z n +hq3); q4=g(x n+h, y n +hk3, z n +hq3);
Для системы (1):
Функция f задается следующим образом:
float f(float x,float y,float z)
{float w;
w=z;
return w;
}
Функция g задается следующим образом:
float g(float x,float y,float z)
{float w;
w=2*z+3*y+5*exp(4*x);
return w;
}
Шаг сетки:h=2/n, где n-количество узлов. (рассматривается промежуток [0,2])
Нахождение решения задачи Коши:
yj=u;zj=v; //u,v-начальные условия для U,V, соответственно. u=0;v=0;
for (i=1;i<=n;i++)
{
rk(i-1,yj,zj);
yi=yj+1./6*h*(k1+2*k2+2*k3+k4);
zi=zj+1./6*h*(q1+2*q2+2*q3+q4);
yj=yi;zj=zi;
}
void rk(int k,float uj,float vj, float s)
{
k1=f(a+k*s,uj,vj);
q1=g(a+k*s,uj,vj);
k2=f(a+k*s+0.5*s,uj+0.5*s*k1,vj+0.5*s*q1); q2=g(a+k*s+0.5*s,uj+0.5*s*k1,vj+0.5*s*q1);
k3=f(a+k*s+0.5*s,uj+0.5*s*k2,vj+0.5*s*q2); q3=g(a+k*s+0.5*s,uj+0.5*s*k2,vj+0.5*s*q2);
k4=f(a+k*s+s,uj+s*k3,vj+s*q3); q4=g(a+k*s+s,uj+s*k3,vj+s*q3);}
Погрешность:
При шаге h погрешность численного решения, полученного по методу порядка p, равнялась K, то при шаге h/2 погрешность K1 уменьшается в 2p раз. т.е чтобы определить порядок надо погрешность при N поделить на погрешность при 2N
Получим величину ≈ 2p
· в пространстве С
NormCρ=max ((U(xj)-Uт(xj))2+(V(xj)-Vт(xj))2)1/2=Chs
j
|
N |
NormCρ |
Отношение погр(N)/ погр(2*N) |
|
10 |
26.0654583 |
12.0386496 |
|
20 |
2.1651480 |
13.97974528 |
|
40 |
0.1548775 |
16.5740861 |
|
80 |
0.0093446 |
2.351256825 |
|
160 |
0.0039743 |
0.8049358 |
|
320 |
0.0049374 |
1.6349548 |
|
640 |
0.0030199 |
0.7671125 |
|
1280 |
0.0039366 |
0.5016313 |
|
2560 |
0.0078468 |
1.5758086 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.