Решение задачи Коши для системы. Решение краевой задачи для системы методом стрельбы, страница 2

N	Отношение погр(N)/ погр(2*N)
20	13.9797452
25	14.0546442
27	14.4637764
35	14.8507882
38	15.3580351
39	16.4338437

·  в пространстве L₂

_{b                                          b}

(∫(|U(xj)-Uj|²)dx / ∫|U(xj)|²dx)^1/2≈Ch^s

^{a                                        a}

/*Интеграл считается по составной формуле Симпсона:

_{b                                        N}

∫f(x)dx≈h/6*∑(f(xi-h)+4*f(xi-h/2)+f(xi)), имеющей 4-ый порядок точности.*/

^{a                        i=1}

Интеграл считается по формуле трапеций:

_{b                                                 n-1}

∫f(x)dx≈h*[0.5f(a)+ ∑f(xi)+0.5f(b)], имеющей 2ой порядок точности.

^{a                                                i=1}

Для функции U(x):

N	Отношение погр(N)/ погр(2*N)
10	12,1743383
20	13,9629755
30	14,9480043
40	14,2390394
50	16,4487095
60	15,9773607

Для функции V(x):

N	Отношение погр(N)/ погр(2*N)
10	12.0808964
20	13.9296865
30	15.0786352
40	14.9833374
50	17.7413368
51	15.1940794
54	16.1325951

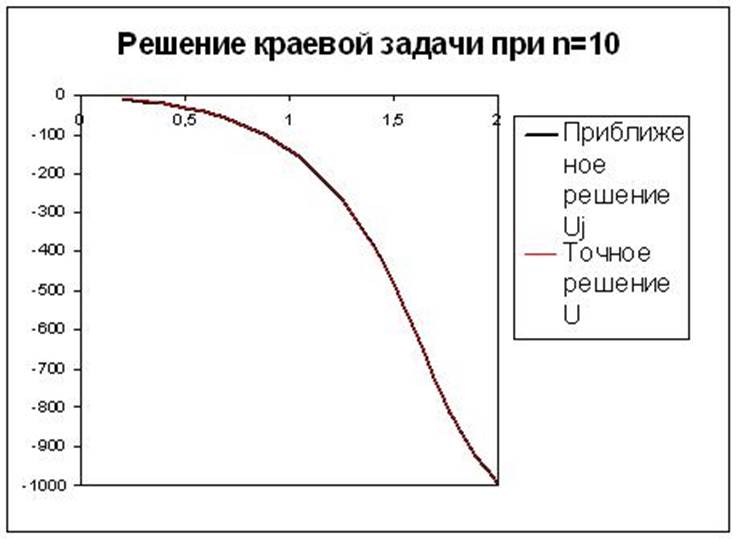
3.  Решение краевой задачи для системы (1) методом стрельбы

Заданы U(0)=2; V(2)=1;

Аналитическое решение:

с1=10.85; с2=-9.85

U=c1*exp(-x)+c2*exp(3x)+exp(4x)                        

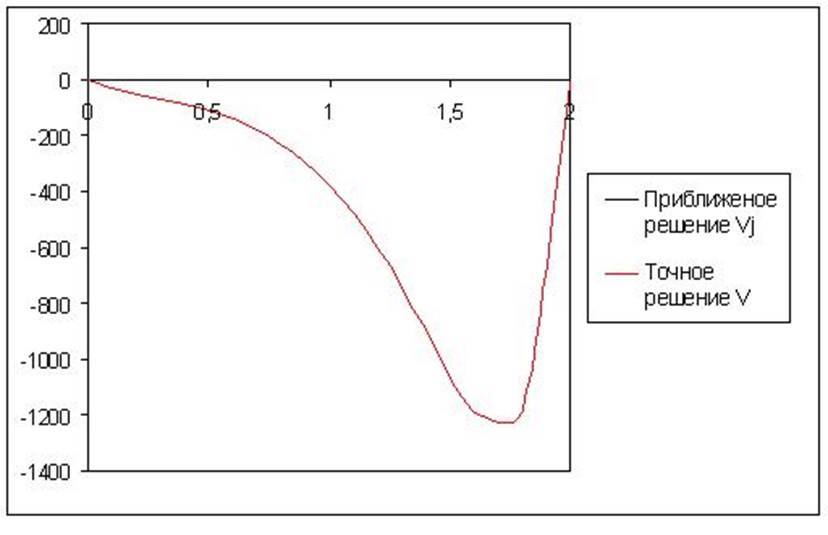
V=-c1*exp(-x)+3*c2*exp(3x)+4*exp(4x).

Метод стрельбы:

x € [a,b]

U’=f(x,U,V)

V’=g(x,U,V)

Краевые условия:

Φ(U(a),V(a))=0;

Ψ(U(b),V(b))=0

Полагаем U(a)=η, где η-параметр. Из левого краевого условия находим V(a)=ξ(η).

Далее решаем задачу Коши с начальными условиями U(a)=η, V(a)=ξ(η).

Решение U(x,η), V(x,η). Необходимо, чтобы решение удовлетворяло правому краевому условию. Обозначим  χ(η)= Ψ(U(b, η),V(b, η))≠0. Находим η при котором χ(η)≈0.

Для системы (1):

Краевые условия имеют вид U(0)=2,V(2)=1;

float U=2; float Vb=1;

c1=9;c2=-40;

Решаем задачу Коши с начальными данными  U(0)=2; V(0)=c1=9;

yj=U;zj=c1;

for (i=1;i<=n;i++)

{

rk(i-1,yj,zj);

yi=yj+1./6*h*(k1+2*k2+2*k3+k4);               

zi=zj+1./6*h*(q1+2*q2+2*q3+q4);    

      yj=yi; zj=zi;

}

Обозначаем z1=V(b,c1);

Аналогично,  z2=V(b,c2);

float fun(float x)

{ float w;

w=Vb-x;

 return w;

}

Для нахождения η при котором V(b)-V(b,η)≈0 применяем метод дихотомии.

с1,с2 подобраны так, чтобы было выполнено fun(z1)*fun(z2)<0.

va=dihot(c1,c2,e,z1,z2);

e=0.001;

float dihot(float a1,float b1, float e,float w1,float w2)

{float yj,zj,zi,yi;int i;

   do

  {   x=(a1+b1)/2;

yj=U;zj=x;

for (i=1;i<=n;i++)

{

rk(i-1,yj,zj);

yi=yj+1./6*h*(k1+2*k2+2*k3+k4);               

zi=zj+1./6*h*(q1+2*q2+2*q3+q4);    

      yj=yi; zj=zi;

}

       if(fun(w2)*fun(zj)<0)

       {a1=x;

      w1=zj;

       }

       else

       {if(fun(w1)*fun(zj)<0) {b1=x;w2=zj;}

       else {

             if (fun(w1)==0)x=a1;

           if (fun(w2)==0)x=b1;

           break;

       } } }

  while(fabs(b1-a1)>e);

  return x;

 }

Т.о нашли η=va при котором выполнено правое краевое условие.

Для нахождения решения краевой задачи решаем задачу Коши с нач.данными:  U(0)=2,V(0)=va.

yj=U;zj=va;

for (i=1;i<=n;i++)

{

rk(i-1,yj,zj);

yi=yj+1./6*h*(k1+2*k2+2*k3+k4);               

zi=zj+1./6*h*(q1+2*q2+2*q3+q4);    

printf("%1.2f   %1.7f   %1.7f    %1.7f",a+i*h,yi,zi,toch1(a+i*h,10.85,-9.85));

printf("\n");

yj=yi;zj=zi;

}