Определенный интеграл. Свойства определенного интеграла. Определенный интеграл с переменным верхним пределом

§5.  Определенный интеграл

5.1. Понятие определенного интеграла

При решении многих задач геометрии, естествознания и техники часто встречаются пределы особого рода сумм (интегральных сумм) – интегралы. Познакомимся с самым простым из интегралов – определенным интегралом.

С его помощью вычисляют площади, ограниченные кривыми, длины дуг, объемы тел, скорость, путь и т.п.

Рассмотрим задачу, приводящую к понятию определенного интеграла.

Рис. 5.1.

Фигура, ограниченная кривой y=f(x) и прямыми   x=a и y=b , называется криволинейной трапецией. Пусть f(x)>0 на [a,b], т.е. выше оси ОХ.

Найдем площадь S данной криволинейной трапеции. Для нахождения S разобьем  отрезок [a,b] произвольным образом на n частей и обозначим точки деления:

a=x₀<x₁<x₂<x₃<...<x_n-1<x_n=b, получим n криволинейных трапеций, т.е. площадь всей криволинейной трапеции будет равна сумме площадей этих трапеций. На отрезках Δx₀, Δx₁, Δx₂, ..., Δx_n-2, Δx_n-1   возьмем произвольные точки C₀, C₁, C₂, ... , C_n-1 и проведем перпендикуляры из этих точек, получим f(C₀), f(C₁), f(C₂), ... , f(C_n-1).

Построим прямоугольники с основаниями Δx₀, Δx₁, Δx₂, ..., Δx_n-2, Δx_n-1  и высотой f(C₀), f(C₁), f(C₂), ... , f(C_n-1).

Площадь ступенчатой фигуры будет приближаться к площади трапеции, если уменьшать Δx_i.

Площадь прямоугольников

S_n = f(C₀) Δx₀ + f(C₁) Δx₁ + ... + f(C_n-1) Δx_n-1 или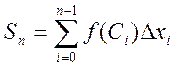 

В пределе при Δx_i→0   получим

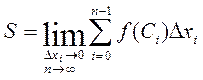
Таким образом мы сделали следующее:

1.  Отрезок [a,b] разбили на n частей.

2.  На каждом интервале взяли точку C_i и вычислили f(C_i).

3.  Составили сумму           

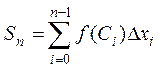
которая называется интегральной суммой для функции y=f(x) на отрезке [a,b].

Если существует конечный предел интегральной суммы, не зависящий от способа разбиения отрезка [a,b] и выбора точек C_i, то этот предел называют определенным интегралом от функции f(x) на отрезке  [a,b] и обозначают:

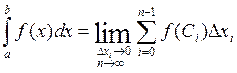
a и b  называют нижним и верхним пределом интегрирования.

Определенный интеграл есть число!

Его значение зависит от вида функции f(x)  и значений верхнего и нижнего пределов, тогда

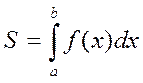
Это геометрический смысл определенного интеграла:  площадь криволинейной трапеции ограниченной функцией f(x) и отрезком [a,b].

	y
				a		b		x

 

Рис. 5.2

5.2. Свойства определенного интеграла

1.  Определенный интеграл не зависит от обозначения переменной интегрирования:

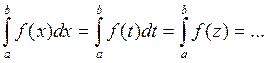
т.к. интегральные суммы представляют собой числа.

2.  Определенный интеграл от суммы конечного числа непрерывных  функций f₁(x), f₂(x), f₃(x), f₄(x), ... , f_n(x), заданных на отрезке [a,b] равен сумме определенных интегралов от слагаемых функций:

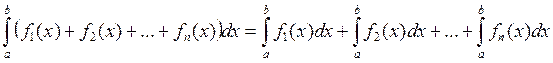
3.  Постоянный множитель можно выносить за знак определенного интеграла:

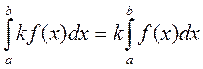
4.  Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл не изменится по абсолютной величине, но изменит знак на противоположный:

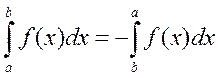
5. 

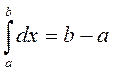
6.  Если существуют интегралы 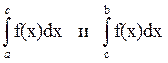 , то существует и 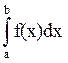и выполняется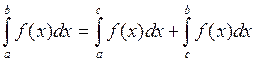 

7.  Если f(x)≥0 , то и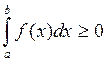 

8.  Если 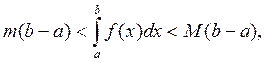    a<b, то m и M соответственно наименьшее и наибольшее значение функции f(x) на отрезке [a,b].

9.  Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке x=c отрезка [a,b] на длину отрезка b-a.

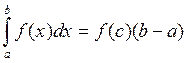
10. 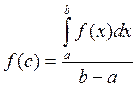   - называют средним значением функции f(x) на отрезке [a,b].

5.3. Определенный интеграл с переменным верхним пределом

Каждому числу x поставим в соответствие число 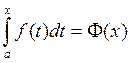 или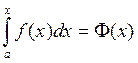

т.е. получили функцию от x. Эту функцию и называют интегралом с переменным верхним пределом.

Теорема: Производная определенного интеграла от непрерывной функции f(x) по его верхнему пределу равна подынтегральной функции с заменой переменной интегрирования верхним пределом, или определенный интеграл с переменным верхним пределом есть первообразная для подынтегральной функции:

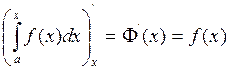
Доказательство:

Дадим приращение Δx, тогда функция получит приращение

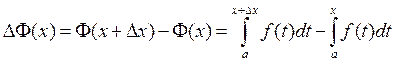
т.к.  , то 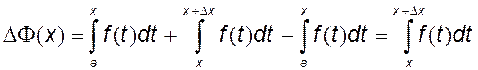. Далее используем свойство 9, согласно которому имеем, разделим на Δх и найдем предел при Δх→0.

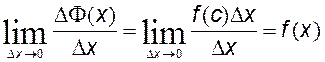, отсюда следует

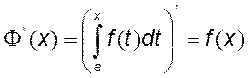
5.4. Формула Ньютона-Лейбница

Теорема: Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования:

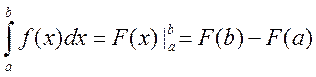
Доказательство:

Рассмотрим интеграл с переменным верхним пределом 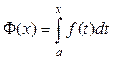. Функция Φ(x) является первообразной для f(x). Пусть F(x) любая первообразная  для f(x) на том же отрезке. Функции Φ(x) и F(x) отличаются на постоянную, тогда 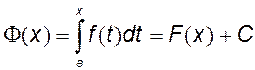. Для нахождения С учтем, что при x=a 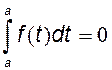 , тогда F(a)+C=0, откуда C= - F(a).  При x=b получаем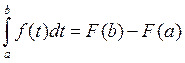  

5.5. Замена переменных интегрирования в определенных интегралах

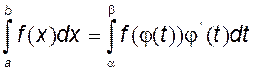
Пример: 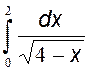 ,     4 - x=t;   dx= - dt; при x₁=0  t₁=4;    при  x₂=2   t₂=2, тогда

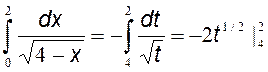
5.6. Интегрирование по частям

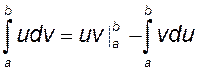
Пример: 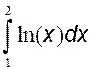 ,    ln(x)=u;   dx=dv; du=dx/x; v=x,    тогда

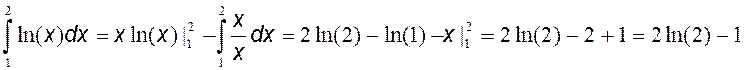
5.7. Вычисление площадей плоских фигур

Если f(x)>0  и площадь фигуры ограничена линиями y=f(x),  x=a  и  x=b , тогда площадь находится через определенный интеграл: 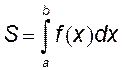 , если , то площадь находится следующим образом: 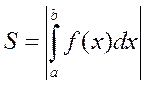. Рассмотрим пример, когда площадь ограничена функцией  y=sin(x),  прямыми  y=0 и x=2π  (см. рисунок рис. 5.3)

x

Рис. 5.3

Общая площадь будет складываться из суммы площадей S₁ и S₂, а они равны:

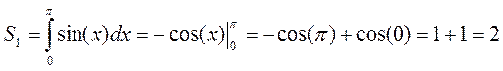
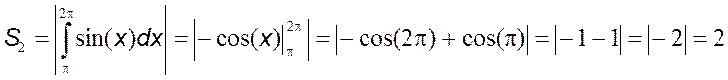
Общая площадь равна S=S₁+S₂=2+2=4    

5.8. Работа переменной силы

Пусть под действием переменной силы F=f(s) тело движется по прямой AB

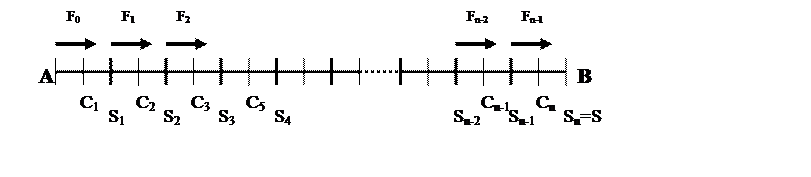
Рис. 5.4

Направление силы совпадает с направлением движения.

Требуется определить работу, производимую силой  F=f(s) при перемещении тела из положения А в положение В.

Разобьем путь АВ на n элементарных отрезков  [s_i-1, s_i] длиной