САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЭЛЕКТРОМЕХАНИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Расчётное задание № 1.
Студент: Батунин О.В.
Группа № 2023/1
Преподаватель: Варламов Юрий Владимирович
Санкт-Петербург
-2004-
ЗАДАНИЕ №1
В линейной электрической цепи, находящейся под действием постоянного напряжения, происходит коммутация.
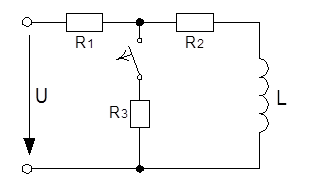
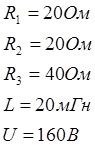
Найти все токи и напряжения на элементах цепи до коммутации и после коммутации. Построить их графики зависимости от времени.
Токи до коммутации: ![]() .
.
Напряжения до коммутации: ![]()
Токи после коммутации: 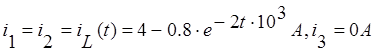 .
.
Напряжение после коммутации: 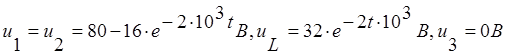
Переменная состояния для данной цепи имеет вид:
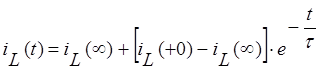 , где
, где 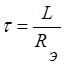 . Определим численные значения
. Определим численные значения
![]() , которые подставим в данную функцию.
, которые подставим в данную функцию.
1.
Определение ![]() .
.
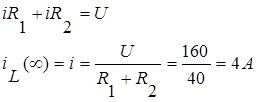
2.
Определение ![]() .
.
По закону коммутации ![]()
![]() .
.
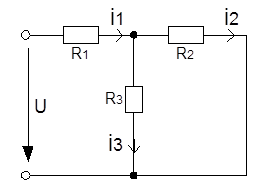
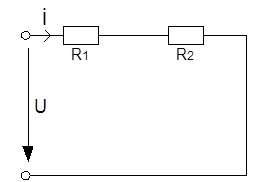
Составим уравнения цепи до коммутации, используя законы Кирхгофа:
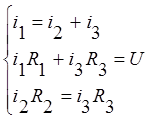
Подставляя первое уравнение системы во второе, и используя третье уравнение, получим:
![]()
Из последнего уравнения системы
выразим ток 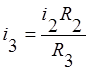 и
подставим его в полученное уравнение, выразим
и
подставим его в полученное уравнение, выразим ![]() :
:
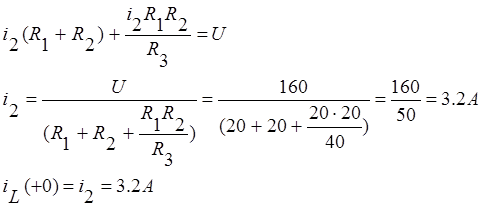
3. Определение постоянной времени t.
Закоротим источники ЭДС, и определим эквивалентное сопротивление цепи относительно зажимов катушки.
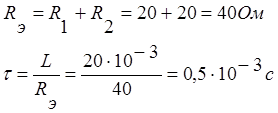

4. Запишем окончательно найденное численное значение переменной состояния
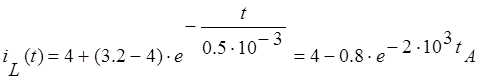
5.
Определение ![]() .
.
Найдём с помощью
дифференцирования ![]() напряжение на катушке в
переходном процессе.
напряжение на катушке в
переходном процессе.
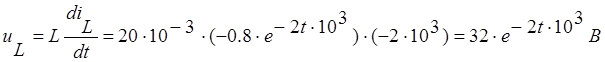
Расчет токов и напряжений после коммутации.
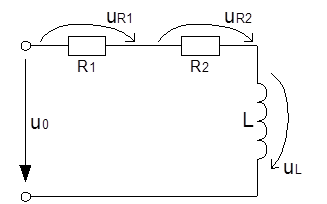
Запишем уравнения Кирхгофа:
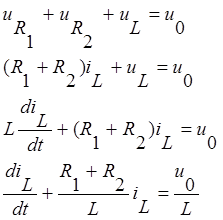
Запишем решение данного дифференциального уравнения в общем виде:
![]()
Запишем характеристический многочлен.
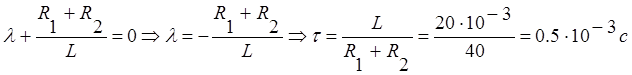
Цепь питается от источника
постоянного тока. Значит при ![]() в цепи
устанавливается постоянный ток, и падение напряжение на катушке будет равно
нулю. Таким образом всё напряжение источника будет приложено к резисторам R1 и R2.
Поэтому ток в цепи после коммутации при установившемся режиме будет равен
в цепи
устанавливается постоянный ток, и падение напряжение на катушке будет равно
нулю. Таким образом всё напряжение источника будет приложено к резисторам R1 и R2.
Поэтому ток в цепи после коммутации при установившемся режиме будет равен 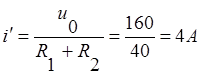 .
.
Для определения постоянной А
запишем общее решение дифференциального уравнения, используя полученное
значение тока в установившемся режиме: 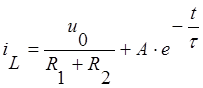
Используем закон коммутации —
непрерывность тока в момент коммутации, и найденное ранее значение ![]() , получим:
, получим:
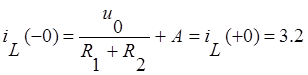 ,
откуда
,
откуда 
Запишем окончательно решение дифференциального уравнения:
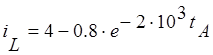
Дифференцированием найдём: 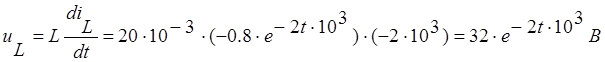
При коммутации размыкается ветвь с сопротивлением R3, поэтому ток i3
после коммутации равен нулю. Таким образом получаем цепь с одним контуром, в
которой токи i1 и i2
будут равны контурному току: ![]() .
.
Рассчитаем напряжения на резисторах после коммутации.
На резисторе R1:
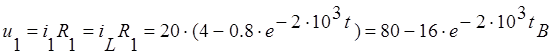
На резисторе R2:
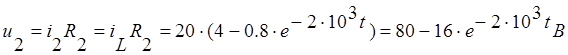
На выводах резистора R3 напряжение после коммутации будет равно нулю,
так как после коммутации ветвь с резистором размыкается и ток в ветви ![]() , следовательно и
, следовательно и ![]() .
.
Расчет токов и напряжений до коммутации.

Составим уравнения цепи до коммутации, используя законы Кирхгофа:
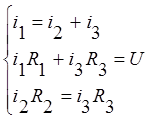
Подставляя первое уравнение системы во второе, и используя третье уравнение, получим:
![]()
Из последнего уравнения системы
выразим ток 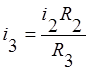 и
подставим его в полученное уравнение, выразим
и
подставим его в полученное уравнение, выразим ![]() :
:
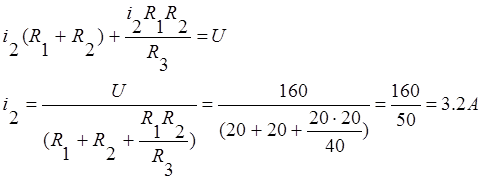
Из последнего уравнения системы получим:
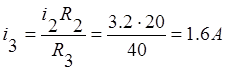
По первому уравнению системы найдём ток ![]() :
:
![]()
Расчёт напряжений на резисторах до коммутации.
На резисторе R1:
![]()
На резисторе R2:
![]()
На резисторе R3:
![]()
Напряжение на катушке до
коммутации равно нулю, так как в установившемся режиме на постоянном токе
сопротивление катушки носит чисто активный характер, а активное сопротивление
катушки ![]() .
.![]()
ЗАДАНИЕ №2
Вариант № 24
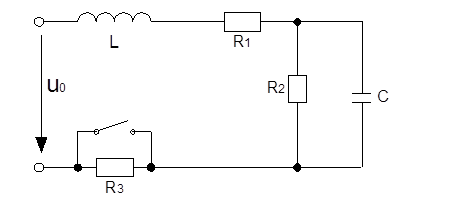
R1=300 Ом
R2=200 Ом
R3=100 Ом
u0=150 В
L=400 млГн
C=40 мкФ
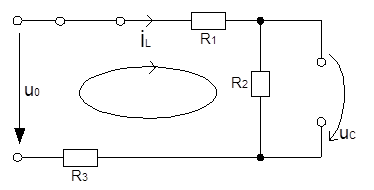
В цепи, находящейся под действием постоянного тока, происходит коммутация в момент времени t=0. Определить напряжения и токи на катушке индуктивности и конденсаторе при t<0, t=0, t>0, применяя:
классический метод,
метод переменных состояния,
метод эквивалентных источников.
Построить графики определённых в расчёте величин.
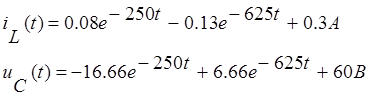
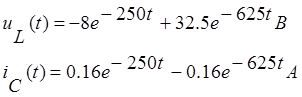
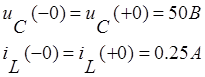
Ток на конденсаторе до коммутации: ![]()
Напряжение на катушке до коммутации: ![]()
Расчёт переменных состояния до коммутации.
![]()
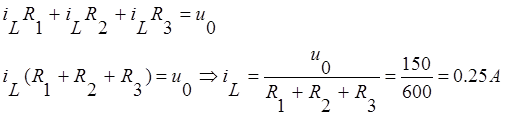
![]()
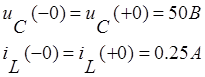
Ток iC на конденсаторе до коммутации равен нулю, так
как конденсатор в установившемся режиме на постоянном токе представляет разрыв
цепи. ![]()
Напряжение на
катушке до коммутации равно нулю, так как в установившемся режиме на постоянном
токе сопротивление катушки носит чисто активный характер, а активное
сопротивление катушки ![]() .
.![]()
Расчёт переменных состояния в установившемся режиме.
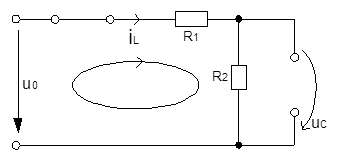
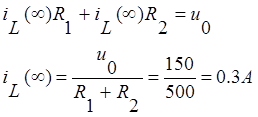
![]()
![]()
Формирование уравнений состояния по методу переменных состояния.
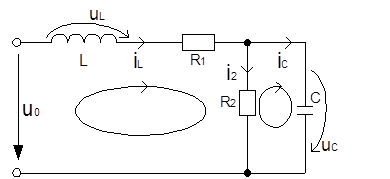
Составим систему уравнений для цепи после коммутации, используя уравнения Кирхгофа:
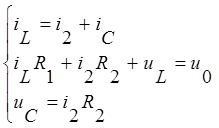
Запишем в этой системе ток на конденсаторе ![]() и
напряжение на катушке
и
напряжение на катушке ![]() через переменные
состояния.
через переменные
состояния.
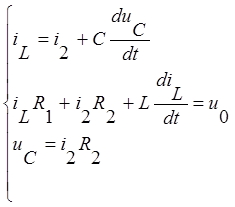
Из третьего уравнения системы выразим ток на резисторе R2: 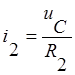 , подставим это
выражение в первое и второе уравнения системы, получим:
, подставим это
выражение в первое и второе уравнения системы, получим:
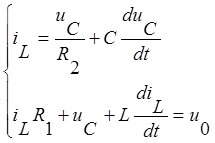
Разрешим полученные уравнения относительно производных.
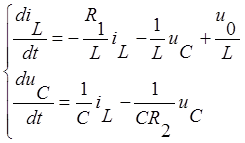
Подставим в систему дифференциальных уравнений численные значения R1, R2, L, C, u0.
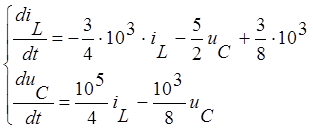
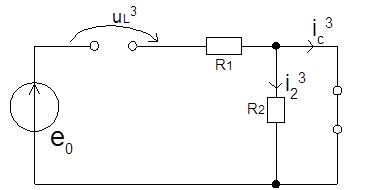
Формирование уравнений состояния с помощью эквивалентных источников.
Заменим динамические элементы в схеме после коммутации эквивалентными источниками: катушки индуктивности — источниками тока, конденсаторы — источниками ЭДС. Получим резистивную цепь.
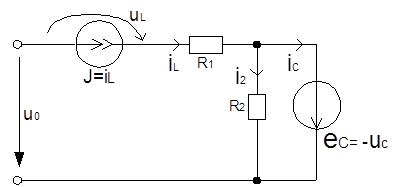
Выразим напряжение uL и ток конденсатора iC через параметры элементов схемы. Структура схемы позволяет воспользоваться принципом наложения. Найдём напряжение uL и ток конденсатора iC при действующим в цепи источнике:
1. eC

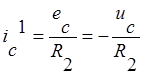
![]()
2. JL
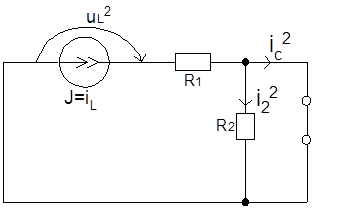
![]()
![]()
![]()
3. e0
![]()
![]()
![]()
Окончательно найдём:
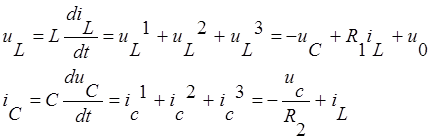
Разрешим полученные уравнения относительно производных.
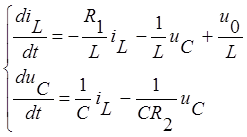
Подставим в систему дифференциальных уравнений численные значения R1, R2, L, C, u0.
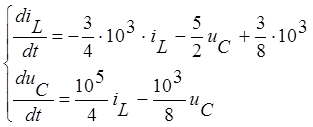
Найдём начальные
условия 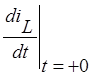 и
и 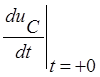 .
.
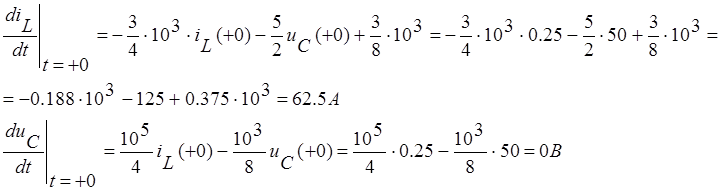
Решение уравнения состояния классическим методом.
Запишем систему дифференциальных уравнений.
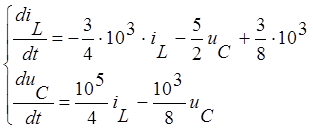
Запишем систему в виде:
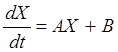 , где
, где 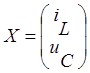 ;
; 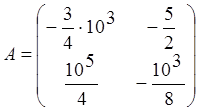 ;
; 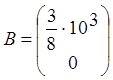
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.