Определение напряжения и токов на элементах цепи до коммутации и после коммутации, а также на катушке индуктивности и конденсаторе при t<0, t=0, t>0, применяя классический метод, метод переменных состояния и метод эквивалентных источников, страница 2

Решение дифференциального уравнения можно записать в виде:

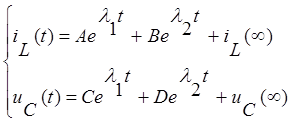
 — корни характеристического уравнения. Они совпадают с собственными числами матрицы А, следовательно могут быть найдены из уравнения:

, где Е — единичная матрица.

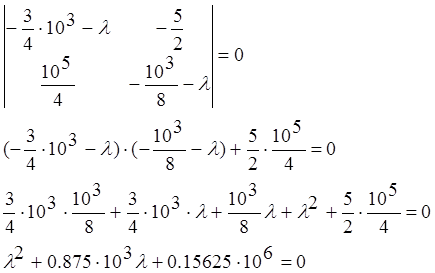
Найдём корни полученного квадратного уравнения.

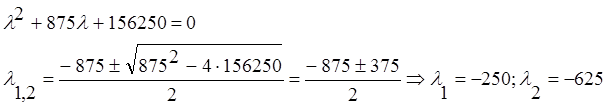
Подставим полученные корни уравнения, значения тока на катушке   и напряжение на конденсаторе , найденные ранее, в решение дифференциального уравнения.

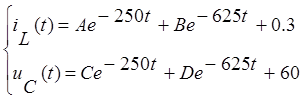
Найдем производную от полученной системы.

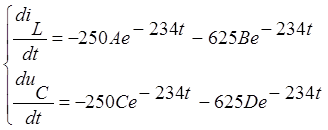
Используя начальные условия запишем:

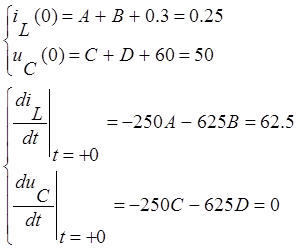
Перепишем эту систему:

;           

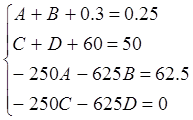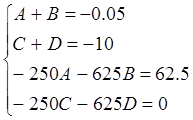
Решим систему этих уравнений:

Из последнего уравнения системы выраз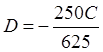им , подставим его во второе уравнение системы, получим:

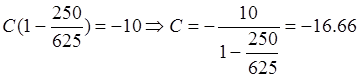
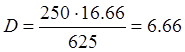
Из первого уравнения системы выразим , подставим это выражение в третье уравнение системы, получим:

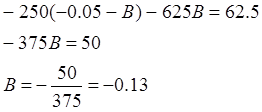
Запишем окончательно решение дифференциального уравнения:

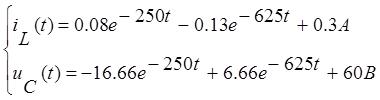
Определим:

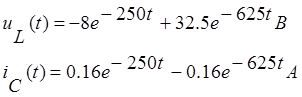
Найдём время переходного процесса:

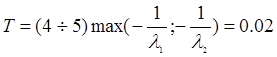
Решение уравнений состояния с помощью матричной экспоненты.

Запишем систему дифференциальных уравнений.

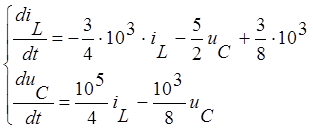
Запишем систему в ви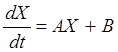де:

, где 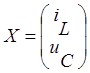 ; ; 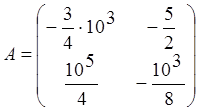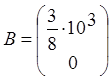, т.е.:

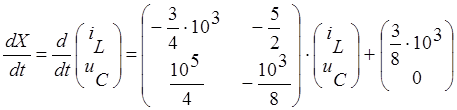
Запишем переменные состояния в ви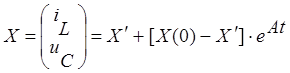де:

, где

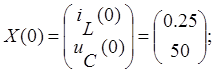
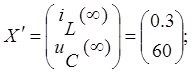
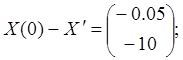
    — матричная экспонента.

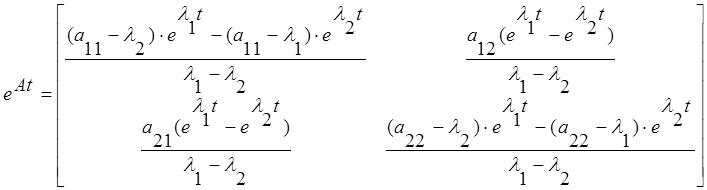
Следовательно:

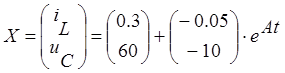
Числа , входящие в матричную экспоненту — корни характеристического уравнения. Они совпадают с собственными числами матрицы А, следовательно могут быть найдены из уравнения:

, где Е — единичная матрица.

Эти корни были найдены в решении уравнений состояния классическим методом, и они равны: .

Подставим значения корней характеристического уравнения и элементы матрицы А в матричную экспоненту, получим:

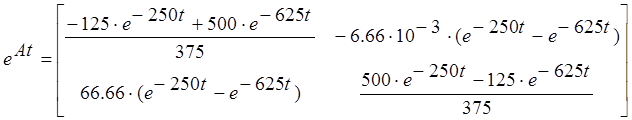, тогда

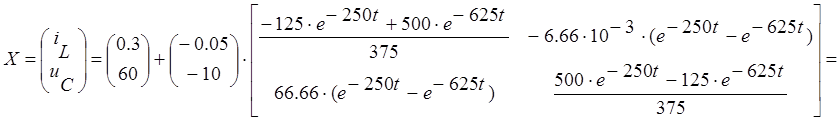
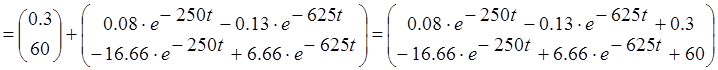
Откуда находим:

Операторный метод.

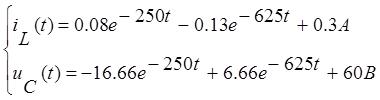
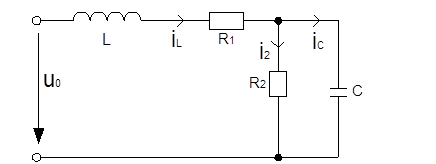
Преобразуем цепь после коммутации согласно правилам для операторного метода.

                    

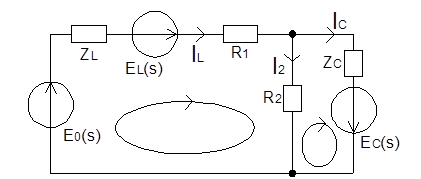
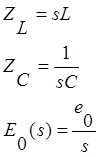
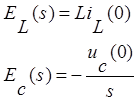
Запишем уравнения Кирхгофа для данной цепи:

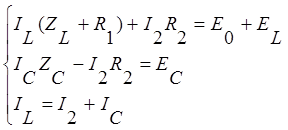
Определение тока :

Подставим третье уравнение системы во второе, и выразим ток :

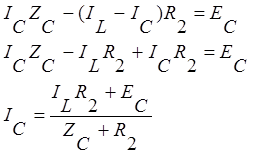
Подставим найденный ток  в третье уравнение системы и выразим из него ток :

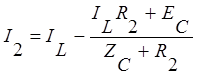
Ток  подставим в первое уравнение системы и выразим из него ток :

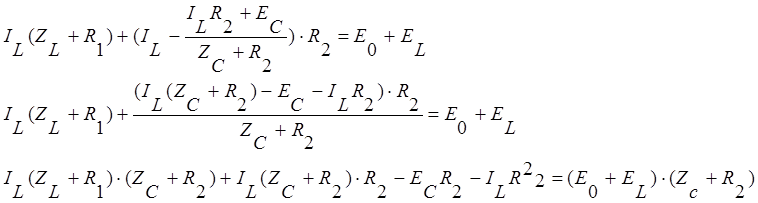
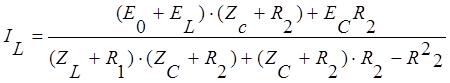
Перепишем это уравнение относительно s:

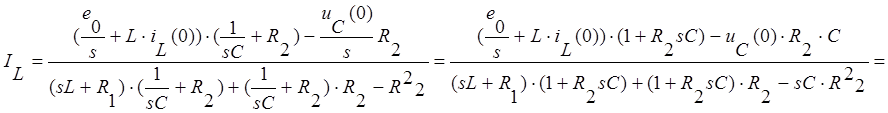
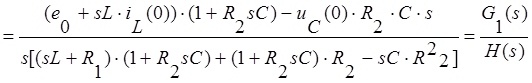
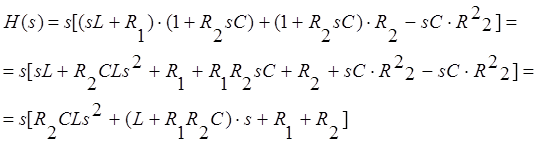
Найдём корни уравнения

Подставим в уравнение численные значения параметров цепи:

 ; ;

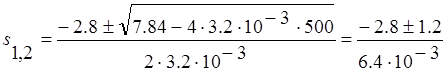
Найдем производную :

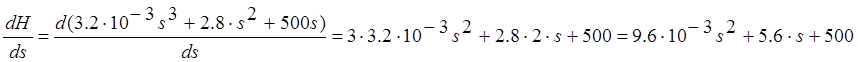
Запишем выражение для числителя:

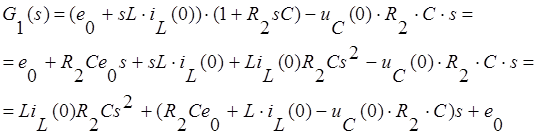
Подставим в уравнение численные значения параметров цепи:

Запишем окончательно по теореме разложения ток :

         Определение напряжения :

Для определения напряжения  определим вначале ток , а потом воспользуемся компонентным уравнением .

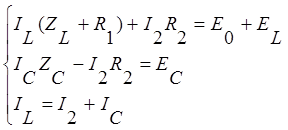
Из первого уравнения системы выразим ток : .

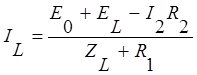Из второго уравнения системы выразим ток : .

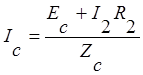Из третьего уравнения системы выразим ток :. В полученное  выражение подставим токи и :

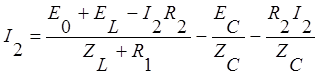, отсюда можем выразить ток  через параметры цепи:

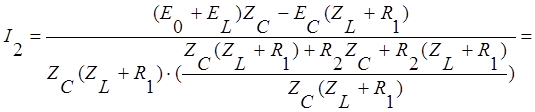
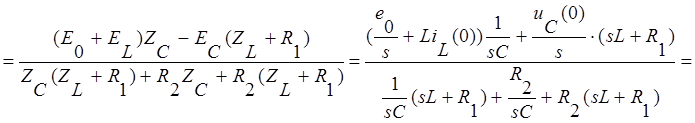
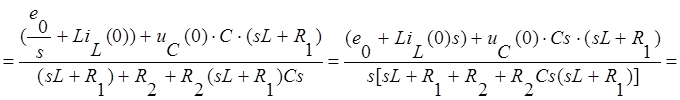
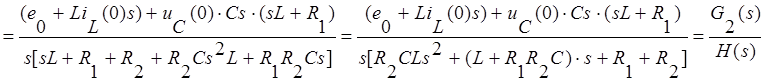
Перепишем числитель этого выражения:

 Подставим в уравнение численные значения параметров цепи:

Знаменатель H(s) полученного выражения совпадает со знаменателем в выражении для тока  при его определении в предыдущем пункте, поэтому, определённые ранее, корни H(s) и значения его производных можно сразу записать в таблицу значений.

Запишем по теореме разложения ток :

Численное интегрирование уравнений состояния.

Запишем уравнения состояния:

,                     

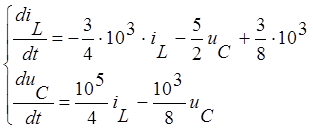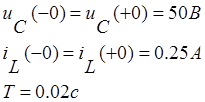
Проведём численное интегрирование уравнений состояния в среде MATLAB 6.1. Для этого создадим m-файл для вычисления значений правых частей (назовём его fun.m). Запишем в этот файл правую часть системы дифференциальных уравнений:

function dydt=fun(t,y)

dydt=[-750*y(1)-2.5*y(2)+375;25000*y(1)-125*y(2)];

где ,.

Сохраним этот файл в каталоге к которому имеет доступ MATLAB. В рабочем окне MATLAB обратимся к процедуре численного интегрирования, сохраняющую результаты интегрирования в рабочем пространстве в виде переменных:

[t,y]=ode45(@fun,[0 0.02],[0.25 50]);

При этом значения t будут выведены в виде вектора-столбца, а y-в виде матрицы.

Теперь для построения графиков переменных состояния можно воспользоваться командой plot:

для построения графика — plot(t,y(:,1))

для построения графика — plot(t,y(:,2)).

	Таблица значений переменных состояния, найденных численным интегрированием в MATLAB.

 

t

0

    0.0002

    0.0004

    0.0006

    0.0008

    0.0012

    0.0016

    0.0019

    0.0023

    0.0027

    0.0031

    0.0035

    0.0039

    0.0044

    0.0049

    0.0054

    0.0059

    0.0064

    0.0069

    0.0074

    0.0079

    0.0084

    0.0089

    0.0094

    0.0099

    0.0104

    0.0109

    0.0114

    0.0119

    0.0124

    0.0129

    0.0134

    0.0139

    0.0144

    0.0149

    0.0154

    0.0159

    0.0164

    0.0169

    0.0174

    0.0179

    0.0184

    0.0190

    0.0195

    0.0200

y(1)         y(2)

    0.2500   50.0000

    0.2617   50.0297

    0.2717   50.1122

    0.2802   50.2388

    0.2875   50.4014

    0.2983   50.7765

    0.3061   51.2195

    0.3115   51.7055

    0.3152   52.2110

    0.3178   52.7643

    0.3193   53.3100

    0.3198   53.8402

    0.3197   54.3462

    0.3192   54.9152

    0.3182   55.4412

    0.3170   55.9248

    0.3157   56.3645

    0.3143   56.7661

    0.3130   57.1274

    0.3118   57.4518

    0.3106   57.7417

    0.3095   57.9997

    0.3085   58.2294

    0.3075   58.4337

    0.3067   58.6150

    0.3060   58.7756

    0.3053   58.9179

    0.3047   59.0440

    0.3042   59.1555

    0.3037   59.2541

    0.3033   59.3413

    0.3029   59.4184

    0.3026   59.4865

    0.3023   59.5467

    0.3020   59.5998

    0.3018   59.6467

    0.3016   59.6882

    0.3014   59.7248

    0.3012   59.7571

    0.3011   59.7856

    0.3009   59.8108

    0.3008   59.8339

    0.3007   59.8542

    0.3006   59.8721

    0.3006   59.8877