Моделювання процесів в електричній системі: Навчальний посібник, страница 6

Таким чином, схема заміщення ділянки довгої лінії може бути представлена в однофазному зображені в симетричному режимі або трьома однаковими схемами заміщення в однофазному зображені в несиметричному режимі (рис. 3.2)

 

Рис. 3.2 – Схема заміщення ЛЕП в однофазному зображені

В усталеному режимі математичну модель довгої лінії можна відобразити рівняннями чотирьохполюсника

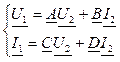                                         ,                                         (3.7)

де А, B, C, D – узагальнені параметри лінії, що залежать від іі параметрів: , ,  (l – довжина лінії), , де , .

При спрощених обчисленнях  для ЛЕП довжиною до 1000 км використовують схему заміщення із зосередженими параметрами (рис. 3.3)

 

Рис. 3.3 – Однолінійна схема заміщення ЛЕП із зосередженими параметрами

Параметри лінії до 300 км визначаються як

 ,

,

,

де R_пит – питомий активний опір.

Параметри лінії від 300 км до 1000 км визначаються як

,

,

.

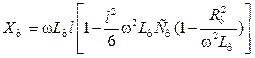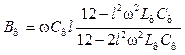В найпростішому випадку в симетричному режимі ЛЕП може бути представлена активним та індуктивним опором, тобто математична модель визначиться першим рівняння системи (3.5).

3.2 Математична модель однофазного двохобмоткового трансформатора

З метою економічної передачі електроенергії на довгі відстані і розподіл її між різноманітними споживачами з¢является необхідність в її трансформації. Останнє здійснюється за допомогою трансформаторів.

Розгляд математичних моделей трансформаторів зручніше розпочати з математичної моделі однофазного двохобмоткового трансформатора, принципова схема якого представлена на рис.3.4.

 

Рис. 3.4 – Принципова схема однофазного двохобмоткового трансформатора

Якщо первинну обмотку трансформатора з числом витків W₁ ввімкнути в мережу, то змінна напруга  U₁ обумовить в ній струм I₁ та магніторушійна сила I₁W₁ створить змінний магнітний потік. Цей магнітний потік створить в обмотці  W₁ ЕРС E₁, а вобмотці W₂ ЕРС  E₂. При роботі трансформатора на холостому ході U₂=E₂. При підключенні до вторинної обмоткиW₂  навантаженя, ЕРСE₂ обумовить протікання струмуI_2. Співвідношення між первинною та вторинною напругою визначиться як W₁U₂=W₂U₁.

Схема заміщення елементу такого трансформатора довжиною dx при умові, що всі взаємоіндуктивності не залежать від частоти та величини струму має вигляд

 

Рис. 3.5 – Схема заміщення елемента трансформатора довжиною dx

Всі елементи представляють питомі значення первинної n та вторинної обмоткb m трансформатора, а саме: С_no, C_mo– ємність між обмоткою трансформатора та землею; С_nm – ємність між первинною та вторинною обмотками трансформатора; С_n, C_m – міжвіткові ємності; ,  – активні опори, що характеризують втрати в осерді; R_n, R_m– активні опори обмоток; L_n, L_m– власні індуктивності обмоток; M_nn, M_mm– міжвиткові індуктивності; M_nm–взаємна індуктивність між обмотками.

Якщо не враховувати активні опори, що характеризують втрати в осерді, і представити трансформатор у вигляді двох елементів, то отримаємо наступну схему заміщення трансформатора

3.3 Математична модель трифазного двохобмоткового трансформатора

Трифазний двох обмотковий трансформатор має три обмотки А, В, С на стороні вищої напруги і три – а, в, с на нижчій стороні (3.4)

 

Рис. 3.4 – Принципова схема трифазного двохобмоткового трансформатора

Якщо знехтувати активними втратами в осерді та ємнісними зв¢язками в трансформаторі, то математична модель трифазного двохобмоткового трансформатора має вигляд

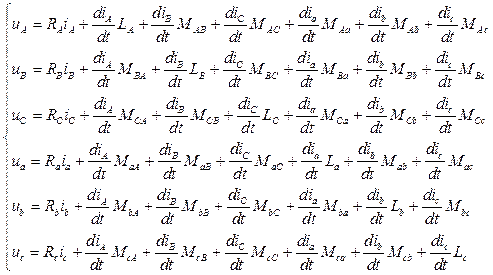. (3.8)

де L_A, L_B, L_C, L_a, L_b, L_c – власні індуктивності обмоток трьох фаз на вищій та нижчій стороні відповідно;

        M_AB= M_BA, M_AC= M_CA, M_BC= M_CB – взаємні індуктивності між фазами вищої сторони,