Моделювання процесів в електричній системі: Навчальний посібник, страница 5

В асинхронних двигунах з фазним ротором статор виконується таким, як у асинхронного двигуна з короткозамкненим ротором, а обмотка збудження виконується трифазною, яка з¢єднана зіркою. За допомогою контактних кілець та щіток в ланцюг ротора вмикають додаткові резистори, які можуть бути або пускові (для збільшення пускового моменту) або регулювальні (для зміни частоти обертання ротора двигуна.  При такому виконанні відсутні обмеження по пусковим моментам, що притаманно асинхронним двигунам з короткозамкненим ротором.  На рис. 2.3 наведено  взаємне розміщення магнітних осей фазових обмоток статора і ротора асинхронного двигуна з фазним ротором.

 

Рис. 2.3 – Взаємне розміщення магнітних осей фазових обмоток статора і ротора асинхронного двигуна з фазним ротором

Рівняння балансу напруг на обмотках статора та ротора записують у вигляді системи

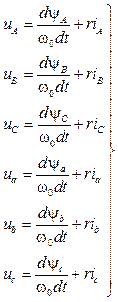,                                   (2.11)

Напруга, що підводиться до двигуна визначається

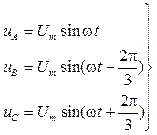                              (2.12)

Потокозчеплення кожної обмотки записується

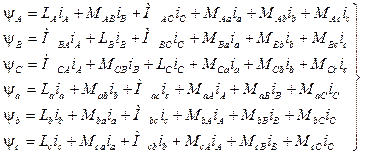.    (2.13)                

З урахуванням  того, що ротори асинхронних двигунів виготовляють симетричними, вирази для визначення індуктивностей та взаємоіндуктивностей обмоток статора мають вигляд

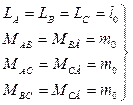                             (2.14)

Індуктивності та взаємоіндуктивності обмоток ротора визначаються

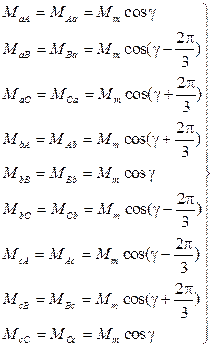,                       (2.15)

де  – кут між магнітними осями фази А статора та ротора,

.

Рівняння руху ротора двигуна аналогічно рівнянню (2.5)

Системи рівнянь (2.11-2.15) та рівняння 2.5 представляють математичну модель асинхронного двигуна з фазним ротором.

Глава 3. Математичні моделі лінії електропередач та силового трансформатора

3.1 Математична модель лінії електропередач

Електрична система має в своєму складі електричну мережу, що зв¢язує джерела і споживачів електроенергії. Основним функціональним елементом мережі є лінії електропередач (ЛЕП) і трансформатори. Головною особливістю ЛЕП є те,що її параметри розподілені рівномірно за всією довжиною.

На рис. 3.1 представлена схема заміщення ділянки лінії довжиною dx

 

Рис.3.1 – Схема заміщення ділянки лінії довжиною dx

Різниця напруг на кінцях ділянки дорівнює падінню напруги в активному опорі та на індуктивностях і визначається як

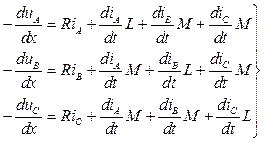                             ,                   (3.1)

де R – активний опір ділянки лінії, що відповідають втратам активної потужності на нагрівання провідників;

    G, G_з – активні провідності, що відповідають втратам на корону;

    С, С_з – ємності, що відповідають електричним зарядам;

    L, M – власна та взаємна індуктивності.

В матричній формі система рівнянь (3.1) запишеться

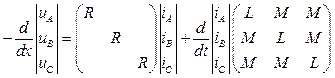                      .         (3.2)

Різниця струмів на початку і в кінці ділянки  дорівнює сумі струмів у провідностях та ємностях і визначається як

.            (3.3)

В матричній формі система рівнянь (3.3) запишеться

         (3.4)

Рівняння (3.1 та 3.4) представляють математичну модель ділянки лінії електропередач.

У випадку, коли розглядається симетричний режим, струм будь-якої  фази можна виразити через струм іншої фази, скориставшись оператором повороту а. Наприклад, струм фаз В и С виразиться через струм фази А наступним чином ,  , з урахуванням цього перше рівняння системи рівнянь (3.1) можна записати

.

Таким чином, для симетричного режиму рівняння зміни струмів і напруги ділянки лінії можна записати для однієї фази

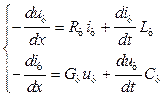                                    ,                                   (3.5)

де,, , .

У випадку, коли розглядається несиметричний режим, рівняння системи (3.5) треба записати окремо для прямої, зворотної та нульової послідовності

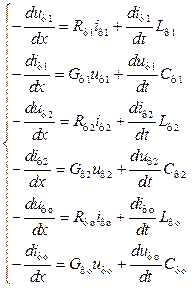                               ,                                  (3.6)

де ,, , , , .