Исследование статической и динамической устойчивости простейшей электрической системы, страница 7

δ(n)	T
18,91	0
19,18017	0,01
19,98242	0,02
21,29231	0,03
23,07022	0,04
25,2629	0,05
27,80569	0,06
30,62504	0,07
33,6414	0,08
36,77218	0,09
39,93469	0,1
43,04876	0,11
46,03898	0,12
48,83645	0,13
51,38	0,14
53,61688	0,15
55,50308	0,16
57,00323	0,17
58,09039	0,18
58,7457	0,19
58,95806	0,2
58,72391	0,21
58,04719	0,22
56,93934	0,23
55,41964	0,24

 

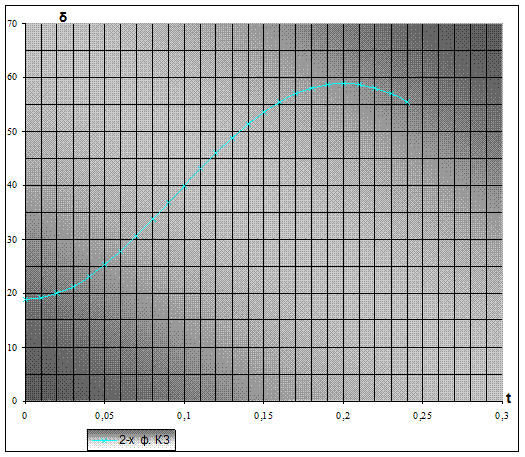
Рис.23 - Зависимость δ = f(t) при 2-х фазном КЗ

2.3.4 Расчёт предельного времени отключения при однофазном КЗ

Так как предельного угла отключения при однофазном КЗ не существует, значит и предельного времени отключения не будет.

Следовательно, методом последовательных интервалов необходимо рассчитать максимальное отклонение угла δ в аварийном режиме.

Расчет угла необходимо вести до тех пор, пока он не начнет уменьшаться.

1-й интервал:

            

Находим прирощение угла δ:

                                

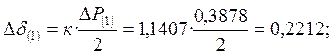
К концу интервала угол δ будет равен:

2-й  интервал.

На всех последующих интервалах ведем расчет по формулам аналогичным формулам второго интервала (63) – (65).

Расчет ведем до тех пор, пока угол не станет больше . По результатам таблицы 11 строим зависимость от t. Рисунок 24.

Таблица 11 - Расчётные данные

δ(n)	t
18,91	0
19,13119	0,01
19,78688	0,02
20,85383	0,03
22,29442	0,04
24,05825	0,05
26,08435	0,06
28,3037	0,07
30,64208	0,08
33,02292	0,09
35,37016	0,1
37,61079	0,11
39,67707	0,12
41,50831	0,13
43,05221	0,14
44,26582	0,15
45,11611	0,16
45,58036	0,17
45,64629	0,18
45,31218	0,19
44,58682	0,2
43,48953	0,21
42,04996	0,22

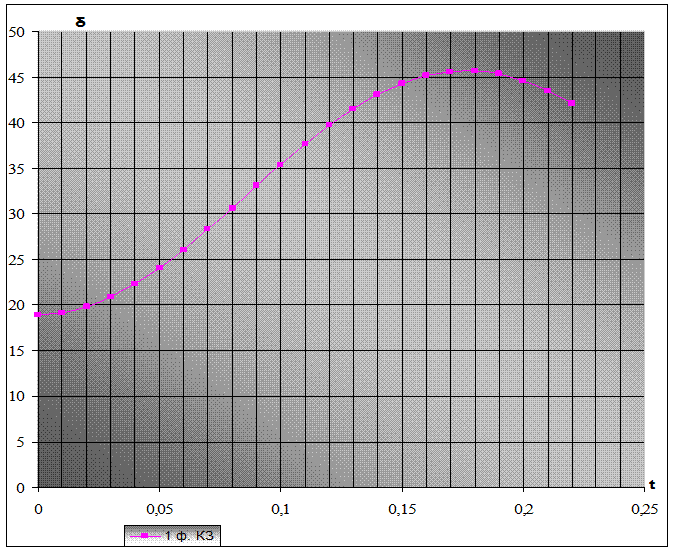
Рис.24 – Зависимость δ = f(t) при однофазном КЗ

По результатам таблиц 8 - 11  строим зависимости от t. Рис.25.

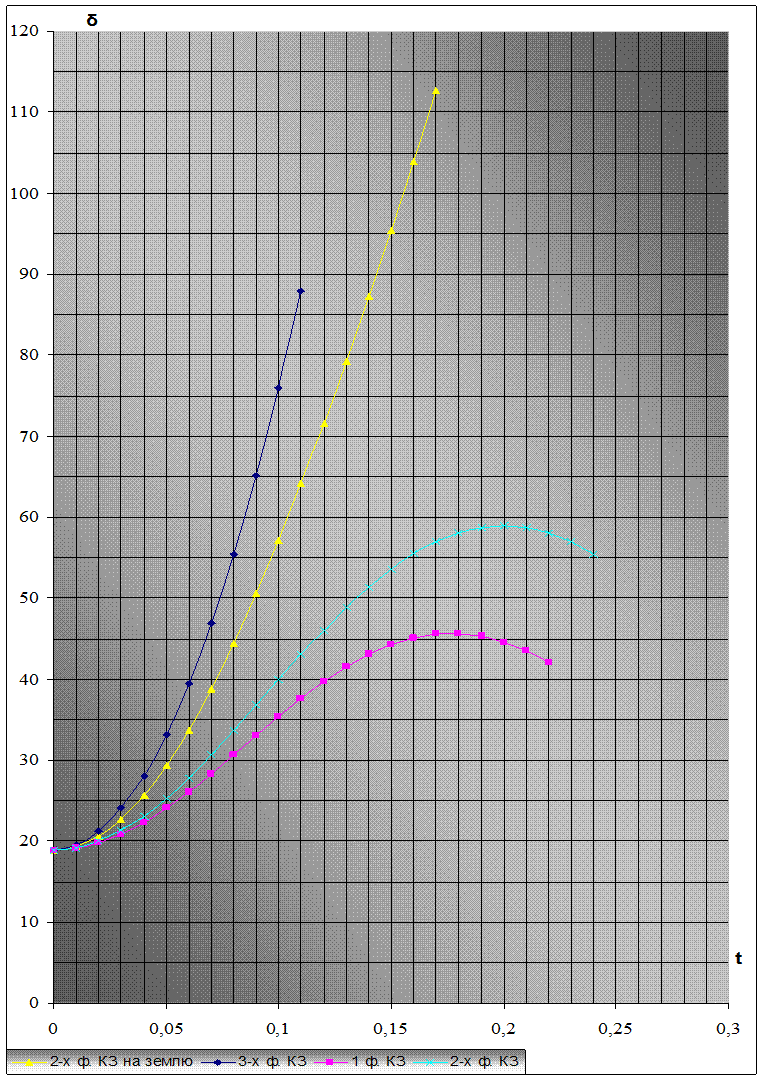
Рис.25 - Зависимость δ = f(t) при всех рассмотренных видах КЗ

Заключение

        В ходе курсового проекта были исследованы статическая и динамическая устойчивость простейшей электрической системы. По результатам полученного расчета можно сделать следующие выводы:

 - исследовав статическую устойчивость системы, можно сделать вывод о том, что наличие у генераторов АРВ обеспечивают расширение зоны устойчивой работы за предел 90°, а наличие нагрузки приводит к уменьшению предела передаваемой мощности и сужение зоны устойчивости работы (рис.11);

 - при исследовании данной электропередачи на динамическую устойчивость, в случае если произошло отключение нижней цепи ЛЭП, площадка ускорения  равна площадки торможения  А_т, что видно из рис.13;

- при двухфазном коротком замыкании на землю, предельное время отключения которого: , в этом случае система оказывается динамически неустойчивой, так как  t_{откл д}> t_{откл пр};

- при трёхфазном коротком замыкании, предельное время отключения которого , так как t_{откл д}> t_{откл пр}, следовательно исследуемая электрическая система может быть динамически не устойчива;

- при двухфазном и однофазном КЗ исходя из  формулы δ_{откл.пр} (формула (57)), функции“arcos” из отрицательного числа больше 1 не существует, следовательно, предельный угол отключения отсутствует, и следовательно,  при этих двух видах КЗ предельное время отключения отсутствует.

Литература

1.  Винославский В.Н. и др. Переходные процессы в системах электроснабжения.- К.: Высшая школа., 1989.- 422 с.

2.  Веников В.А. Переходные электромеханические процессы в электрических системах. - М.: Высшая школа., 1970.- 472 с.

3.  Неклепаев Б.Н., Крючков И.П. Электрическая часть станций и подстанций. - М.: Энергоатомиздат, 1989.- 606 с.

4.  Ульянов С.А. Электромагнитные переходные процессы в электрических системах.- М.: Энергия, 1970.- 520 с.