Принимаем Uб= U0=220 кВ
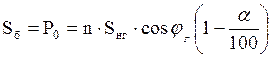 (1)
(1)
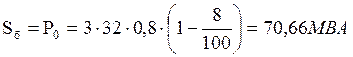
![]() Рассчитываем сопротивления:
Рассчитываем сопротивления:
- генераторов:
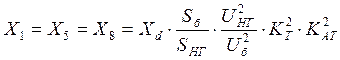 (2)
(2)
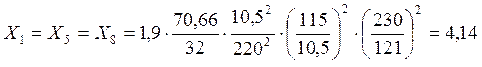
- трансформаторов:
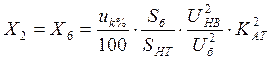 (3)
(3)
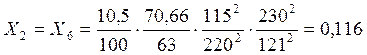
- линии:
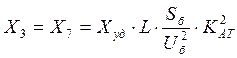 (4)
(4)
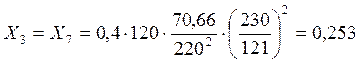
- автотрансформатора:
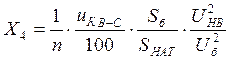 (5)
(5)
где n = 2 – количество автотрансформаторов.
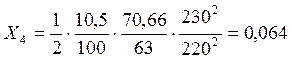
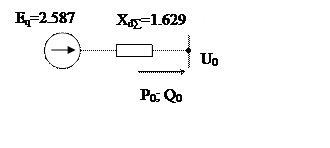 Преобразовываем схему замещения к простейшему виду и находим
сопротивление
Преобразовываем схему замещения к простейшему виду и находим
сопротивление![]() :
:
Рис.3 – Преобразованная схема замещения
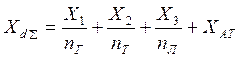 (6)
(6)
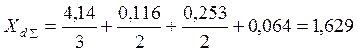
Находим предел передаваемой мощности и предел статической устойчивости данной электрической системы.
Предельное значение мощности наступает при угле δ=90°. Это и будет предел статической устойчивости.
δ пр1=90°
В последней формуле все величины должны быть выражены в относительных единицах:
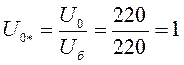
Из векторной диаграммы
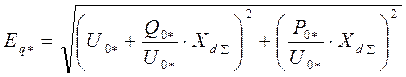 (7)
(7)
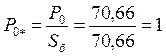
![]()
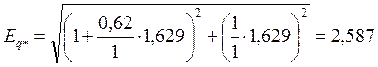
Тогда предел передаваемой мощности для электрической системы с нерегулируемыми генераторами
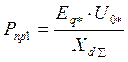 (8)
(8)
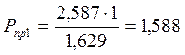
Рассчитываем запас статической устойчивости простейшей электрической системы с нерегулируемыми генераторами:
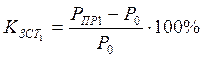 (9)
(9)
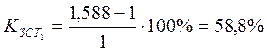
Угловая характеристика мощности будет иметь вид
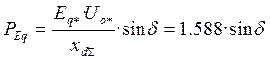 (10)
(10)
Задаваясь
значениями угла ![]() от 0° до 180°(подставив их в
формулу (10)) мы получим соответствующие значения
от 0° до 180°(подставив их в
формулу (10)) мы получим соответствующие значения ![]() .
Результаты расчетов заносим в таблицу 2.
.
Результаты расчетов заносим в таблицу 2.
1.1.2 Генераторы ЭС с АРВ пропорционального действия
Схема замещения электропередачи с генераторами, имеющими АРВ пропорционального действия (п.д.) при о.н., изображена на рисунке 4.
Сопротивления всех элементов, кроме сопротивлений генераторов, остаются такими, как и в предыдущей задаче.
Генераторы ЭС с АРВ п.д. вводят в
схему замещения ЭДС ![]() и сопротивление
и сопротивление ![]() .
.
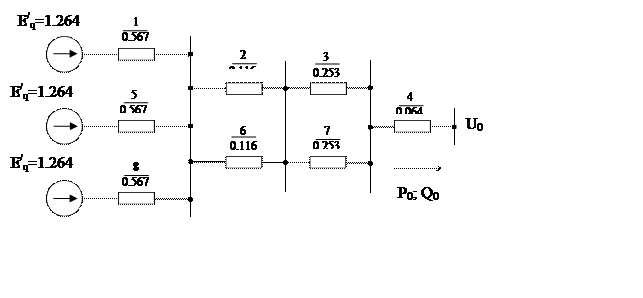
Рис. 4 - Схема замещения электропередачи с генераторами, имеющими АРВ п.д. при о.н.
Определяем относительное
сопротивление генератора ![]() , с АРВ п.д. по формуле:
, с АРВ п.д. по формуле:
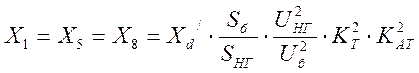 (11)
(11)
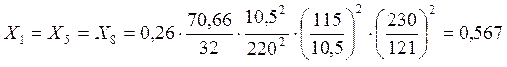
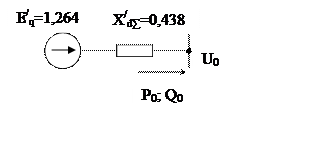 Преобразуем схему
замещения к простейшему виду и определяем суммарное сопротивление передачи по
формуле (6).
Преобразуем схему
замещения к простейшему виду и определяем суммарное сопротивление передачи по
формуле (6).
Рис.5 – Преобразованная схема замещения
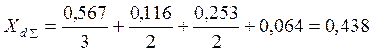
Угловую характеристику мощности рассчитываем по формуле (12):
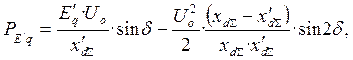 (12)
(12)
Расчетную ЭДС определяем по формуле (13):
![]() (13)
(13)
где 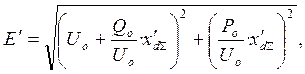 (14)
(14)
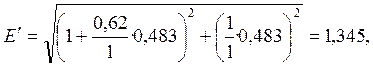
Аргумент определяем по формуле:
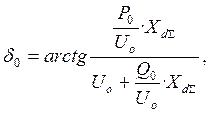 (15)
(15)
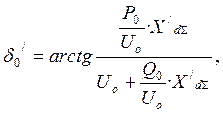 (16)
(16)
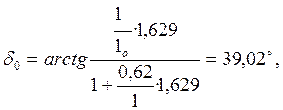
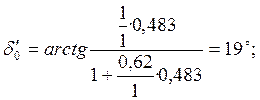
Тогда расчетная ЭДС согласно формуле (13) будет равна
![]()
Следовательно, согласно формуле (12), угловая характеристика мощности ЭС с АРВ п.д. будет иметь вид
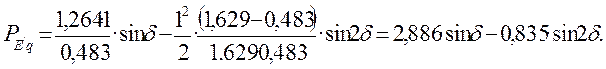 (17)
(17)
Задаваясь
значениями угла ![]() от 0° до 180°(подставив их в
формулу (17)) мы получим соответствующие значения
от 0° до 180°(подставив их в
формулу (17)) мы получим соответствующие значения ![]() .
Результаты расчетов заносим в таблицу 2.
.
Результаты расчетов заносим в таблицу 2.
Обозначим,
что ![]() =2,886,
=2,886, ![]() =0,835
=0,835
Предел статической устойчивости рассчитываем по формуле (18).
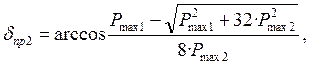 (18)
(18)
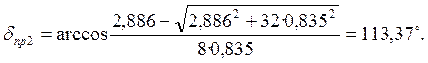
Предел
передаваемой мощности ![]() определяем по формуле (19).
определяем по формуле (19).
![]() (19)
(19)
![]()
Коэффициент
запаса статической устойчивости ![]() , %, определяем по
формуле (9).
, %, определяем по
формуле (9).
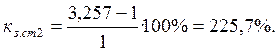
1.1.3 Генераторы ЭС с АРВ сильного действия.
Генераторы ЭС с АРВ сильного действия.
в схеме замещения задаются ![]() и сопротивление генераторов
и сопротивление генераторов
![]() . Далее расчет ведем аналогично расчету
1.1.2.
. Далее расчет ведем аналогично расчету
1.1.2.
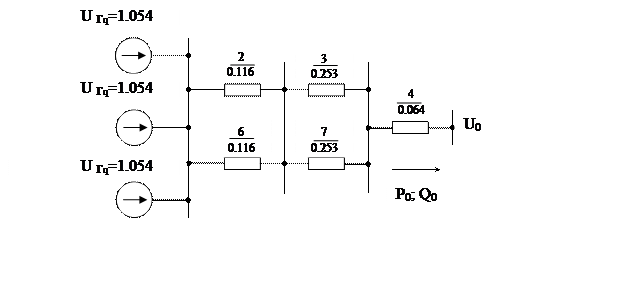
Рис.6 – Схема замещения передачи с АРВ с.д.
Сопротивления всех элементов берем из предыдущей задачи (1.1.2)
Преобразуем схему замещения к простейшему виду.
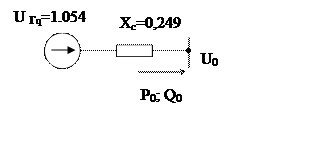
Рис. 7– Преобразованная схема замещения
Определяем сопротивление связи.
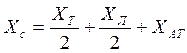 (20)
(20)
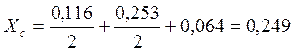
Значения ![]() и
и ![]() берем из задачи 1.1.1
берем из задачи 1.1.1
Определяем модуль ![]() ,
,
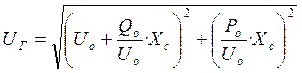 (21)
(21)
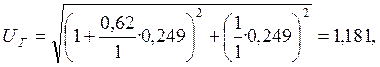
Аргумент
![]() берем из
задачи 1.1.2.
берем из
задачи 1.1.2.
Аргумент δс определяем по формуле (22):
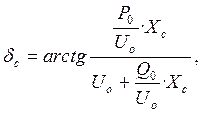 (22)
(22)
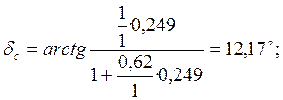
Определяем расчетную величину ![]() , по формуле
, по формуле
![]() =Uг∙cos(δ0
–δс) (23)
=Uг∙cos(δ0
–δс) (23)
![]() = 1,181∙cos(39,02°
– 12,17°)=1,054
= 1,181∙cos(39,02°
– 12,17°)=1,054
Определяем угловую характеристику мощности передачи с генераторами с АРВ с.д.
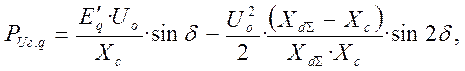 (24)
(24)
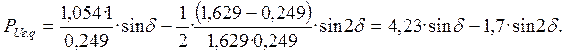
![]() (25)
(25)
Обозначим,
что ![]() =4,23,
=4,23, ![]() =1,7
=1,7
Предел
статической устойчивости ![]() , определим по формуле
, определим по формуле
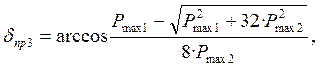 (26)
(26)
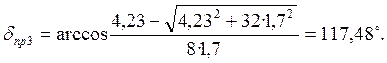
Следовательно, предел передаваемой мощности ![]() будет
равен :
будет
равен :
![]()
Коэффициент запаса статической устойчивости ![]() , %, определяем по формуле
, %, определяем по формуле
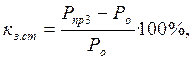 (27)
(27)
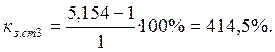
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.