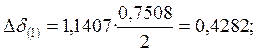
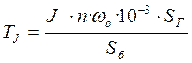 (61)
(61)
-постоянная инерции эквивалентного генератора;
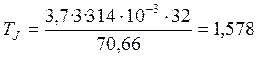
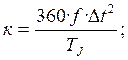 (62)
(62)
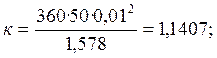
К концу интервала угол δ будет равен:
![]()
2-й интервал.
![]() (63)
(63)
![]()
![]() (64)
(64)
![]()
![]() (65)
(65)
![]()
На всех последующих интервалах ведем расчет по формулам аналогичным формулам второго интервала (63) – (65).
Расчет ведем до тех пор, пока угол ![]() не станет больше
не станет больше ![]() .
По результатам таблицы 8 строим зависимость
.
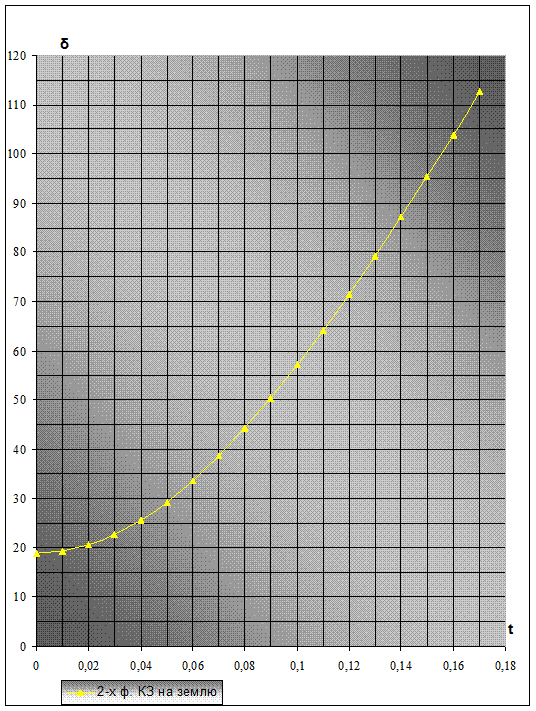
По результатам таблицы 8 строим зависимость ![]() от t.
Рисунок 21.
от t.
Рисунок 21.
![]()
![]()
Рис. 21 – Зависимость δ = f(t) при 2-х фазном КЗ на землю
Таблица 8 - Расчётные данные
|
δ(n) |
t |
|
18,91 |
0 |
|
19,33821 |
0,01 |
|
20,61664 |
0,02 |
|
22,72689 |
0,03 |
|
25,63895 |
0,04 |
|
29,31215 |
0,05 |
|
33,6966 |
0,06 |
|
38,73508 |
0,07 |
|
44,36539 |
0,08 |
|
50,52302 |
0,09 |
|
57,14427 |
0,1 |
|
64,16934 |
0,11 |
|
71,54555 |
0,12 |
|
79,23037 |
0,13 |
|
87,19415 |
0,14 |
|
95,42248 |
0,15 |
|
103,9182 |
0,16 |
|
112,7032 |
0,17 |
По построенной кривой и рассчитанному ранее предельному углу отключения находим tоткл пр
tоткл пр=0,168.
Рассчитываем действительное время отключения
tоткл д= tрз+ tов=0,08+0,1=0,18с
Сравнив предельное время отключения и действительное сделаем вывод, что система динамически не устойчива при двухфазном КЗ на землю так как tоткл д> tоткл пр
0,18 >0,168
2.3.2 Расчёт предельного времени отключения при трёхфазном КЗ
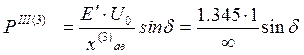 =0sin δ=0 (66)
=0sin δ=0 (66)
Из формулы (66) следует, что
![]()
1-ый интервал:
Находим прирощение угла δ:
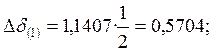
К концу интервала угол δ будет равен:
![]()
2-й интервал.
![]()
![]()
![]()
На всех последующих интервалах ведем расчет по формулам аналогичным формулам второго интервала (63) – (65).
Расчет ведем до тех пор, пока угол ![]() не станет больше
не станет больше ![]() .
По результатам таблицы 9 строим зависимость
.
По результатам таблицы 9 строим зависимость ![]() от t..
Рисунок 22.
от t..
Рисунок 22.
Таблица 9- Расчётные данные
|
δ(n) |
t |
|
18,91 |
0 |
|
19,48035 |
0,01 |
|
21,1914 |
0,02 |
|
24,04315 |
0,03 |
|
28,0356 |
0,04 |
|
33,16875 |
0,05 |
|
39,4426 |
0,06 |
|
46,85715 |
0,07 |
|
55,4124 |
0,08 |
|
65,10835 |
0,09 |
|
75,945 |
0,1 |
|
87,92235 |
0,11 |
![]()
![]()
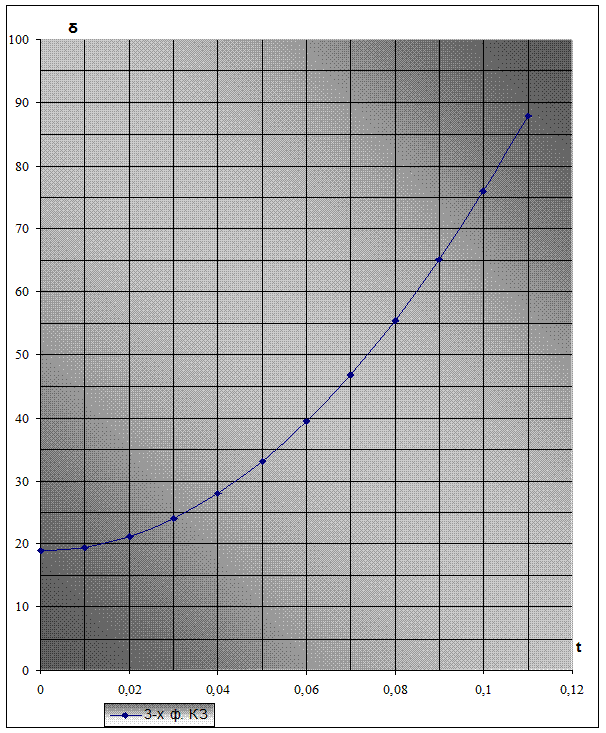
Рис. 22 - Зависимость δ = f(t) при 3-х фазном КЗ
По построенной кривой и рассчитанному ранее предельному углу отключения находим tоткл пр
tоткл пр=0,108 с.
Рассчитываем действительное время отключения
tоткл д= tрз+ tов=0,08+0,1=0,18с
Сравнив предельное время отключения и действительное сделаем вывод, что система динамически не устойчива при трехфазном КЗ так как tоткл д> tоткл пр
0,18 >0,108 с.
2.3.3 Расчёт предельного времени отключения при двухфазном КЗ
Так как предельного угла отключения при двухфазном КЗ не существует, значит и предельного времени отключения не будет. Следовательно, методом последовательных интервалов необходимо рассчитать максимальное отклонение угла δ в аварийном режиме.
Расчет угла необходимо вести до тех пор, пока он не начнет уменьшаться.
1-й интервал:
![]()
Находим прирощение угла δ:
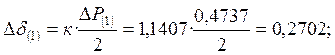
К концу интервала угол δ будет равен:
![]()
2-й интервал.
![]()
![]()
![]()
На всех последующих интервалах ведем расчет по формулам аналогичным формулам второго интервала (63) – (65).
Расчет ведем до тех пор,
пока угол ![]() не станет больше
не станет больше ![]() .
По результатам таблицы 10 строим зависимость
.
По результатам таблицы 10 строим зависимость ![]() от t..
Рисунок 23.
от t..
Рисунок 23.
Таблица 10: Расчётные данные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.