Исследование статической и динамической устойчивости простейшей электрической системы, страница 3

Задаваясь значениями угла  от 0° до 180°(подставив их в формулу (10)) мы получим соответствующие значения . Результаты расчетов заносим в таблицу 2.

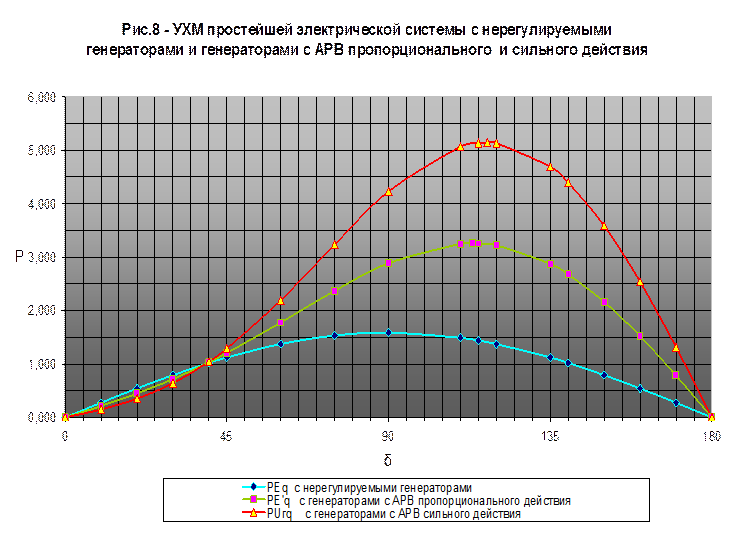
По результатам таблицы 2 строим в одних координатных осях угловые характеристики мощности для ЭС с генераторами без АРВ, с АРВ п.д. и АРВ с.д.

Таблица 2 - Таблица значений УХМ нерегулируемых генераторов, генераторов с АРВ п.д. и с.д.

δ	0	30	45	60	δпр1= 90	δпр2= 113,37	δпр3= 117,48	120	135	180
РЕq	0	0,794	1,123	1,375	1,588	-	-	1,375	1,123	0
PE'q	0	0,72	1,206	1,776	2,886	3,257	-	3,222	2,876	0
PUгq	0	0,64	1,29	2,19	4,23	-	5,14	5,14	4,69	0

  1.2 Определение предела передаваемой мощности с учетом нагрузки (у.н.).

Включение нагрузки превращает исследуемую систему в сложную, и поэтому следует воспользоваться выражением угловой характеристики мощности генератора, работающего в сложной системе, которая после упрощения будет иметь вид:

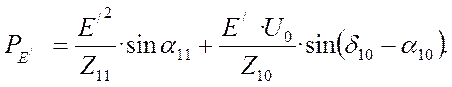     (28)

1.2.1 Генераторы электрической станции (ЭС) с АРВ п. д.  с у.н.

Генератор вводится в схему замещения ЭДС и сопротивлением . Сопротивления всех элементов берем из задачи 1.1.2

Схема замещения электропередачи с генераторами с АРВ пропорционального действия с учётом нагрузки представлена на рис. 9.

 

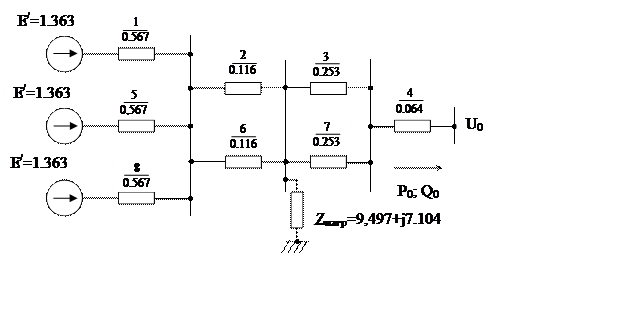
Рис.9 - Схема замещения электропередачи с генераторами с АРВ п.д. с у.н.

Преобразуем схему замещения к виду, представленному на рис. 10.

.

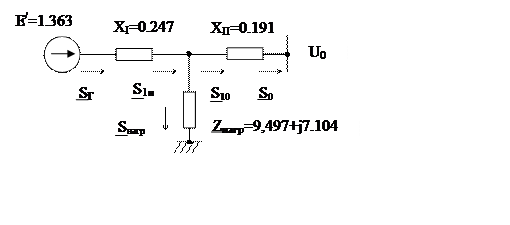
Рис.10 – Преобразованная схема замещения

Где                            

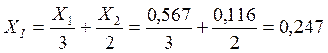
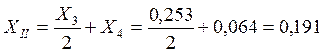
Определим сопротивление нагрузки , по формуле

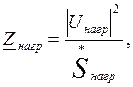                                (29)

где   -  сопряженный комплекс мощности.

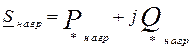                                  (30)

В формуле (30):

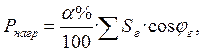                           (31)

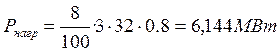
Определим активную мощность нагрузки в относительных единицах , по формуле 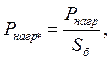(32)

                                     (32)

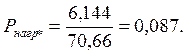
Определим реактивную мощность загрузки в относительных единицах по формуле (33):

                                (33)

Тогда полная мощность нагрузки будет иметь вид:

А сопряженный комплекс мощности:

Рассчитываем напряжение на шинах нагрузки , по формуле 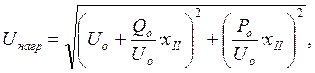(34)

                 (34)

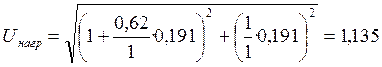
Тогда, согласно формуле (29), сопротивление нагрузки будет равно:

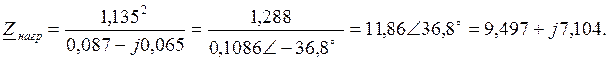
Находим расчетное собственное сопротивление  методом преобразований  по формуле 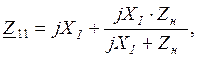(35):

                   (35)

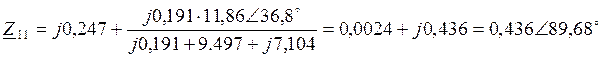
Находим угол  

Находим расчетное взаимное  сопротивление  методом преобразований по формуле 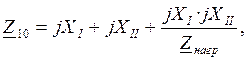(36)

                   (36)

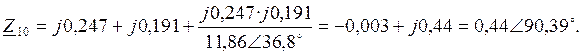
Находим угол  

Обозначим :

 - комплекс мощности поступающей в систему;

 - комплекс мощности вытекающей из узла нагрузки;

 - комплекс мощности нагрузки;

 - комплекс мощности притекающей к узлу нагрузки;

 - комплекс мощности вытекающей из генератора

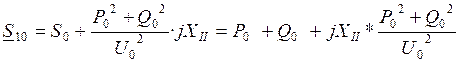Определим мощность генератора, вытекающую из узла нагрузки в систему , по формуле (37)

        (37)

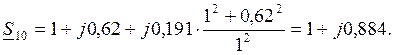
Определим мощность, притекающую к узлу нагрузки от электростанции , по 1-му закону Кирхгофа:

                                 (38)

Определяем комплексное значение напряжения на шинах нагрузки , по формуле

                  (39)

где

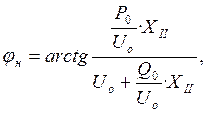                          (40)

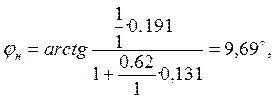
Определяем значение ЭДС  по формуле:

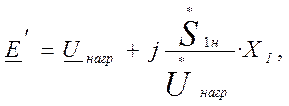                      (41)

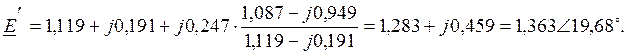
Определим предел статической устойчивости:

                               (42)

Рассчитываем предел передаваемой мощности :

                      (43)

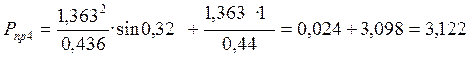
Коэффициент запаса статической устойчивости , %, определяем по формуле

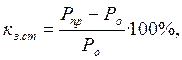                             (44)

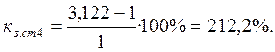
По формуле (28) определяем угловую характеристик мощности электропередачи с генераторами с АРВ п. д . и с у. н.:

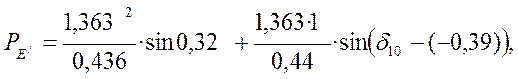
                    (45)

Задаваясь значениями угла  от 0° до 180°(подставив их в формулу (45)) мы получим соответствующие значения . Результаты расчетов заносим в таблицу 3.

Таблица 3 – Значения УХМ простейшей передачи с генераторами с АРВ п. д. с учетом нагрузки.