Импульсные устройства. Электронные триггеры, страница 9

Как было выяснено в предыдущем анализе, основа любого триггера состоит в использовании усилителя с положительной обратной связью, замыкая которую можно получить систему с регенеративным переключением между двумя противоположными стабильными состояниями.  Удобным  элементом для реализации такой задачи является широко распространённая микроэлектронная схема операционного усилителя, условное изображение которого показано на рис.4.15. Операционные  усилители (ОУ) имеют дифференциальные входы, так что выходное напряжение пропорционально разности напряжений на прямом и инверсном входах: . Коэффициент усиления  весьма большой: он составляет величины от до  и даже . Входные сопротивления ОУ за счёт использования на входах  транзисторов в микротоковом режиме  или МДП транзисторов составляют десятки и сотни килоомов, что в практических задачах позволяет не учитывать входные токи. Выходные  цепи (обычно, эмиттерные повторители)  обладают малым выходным сопротивлением, что позволяет моделировать их генераторами напряжения.  Отметим также преимущественное использование ОУ с питанием от биполярных источников  и   .             Перечисленные высокие параметры ОУ в сочетании с функциональными удобствами,  даваемыми дифференциальными входами,  делают ОУ весьма удобным элементом  схемотехники.

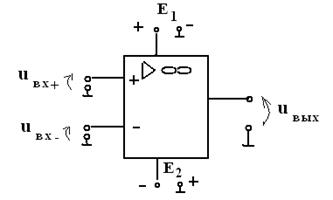
Рис. 4.15

Для реализации схемы триггера ОУ охватывают цепью положительной обратной связи, реализуемой простым резисторным делителем  (рис.4.16).  Благодаря перечисленным достоинствам ОУ формулу для глубины обратной связи можно записать в простой  форме: 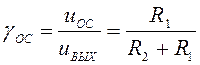. Микроэлектронная или тщательная дискретная  технология изготовления позволяют  не учитывать инерционность цепи обратной связи, или зависимость  от частоты.

Рис. 4.16

Анализ состояния цепей с положительной обратной связью производят с использованием передаточной функции при разомкнутой обратной связи  (рис.4.17).  Такая  схема при замыкании цепи обратной связи останется в покое, если  , что соответствует решению системы уравнений                                   

    .                                              (4.12)

Здесь    - нелинейная зависимость для ОУ с учётом участков перехода его выходных цепей в отсечку или насыщение. На рис.4.18  построена кусочно-линейная аппроксимация этой  зависимости  (при  на рис.4.16), и линейная функция связ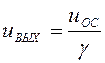и   при , отсчитываемом на одной оси с .  Решение системы (4.12) определяется точками пересечения диаграмм на  рис.4.18, определяющих условие равновесного состояния системы с замкнутой положительной обратной связью .  Таких точек три: «0», «1» и «2».  Их свойства различны.

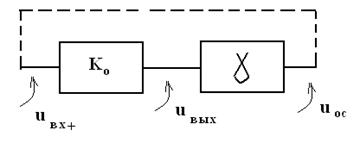
Рис. 4.17

Рис. 4.18

В точке «0» ОУ находится в активном состоянии с коэффициентом усиления  и  при замыкании  положительной обратной связи незначительное отклонение  от нуля приводит  к лавинообразному изменению состояния схемы. Согласно (4.5) для этого необходимо условие 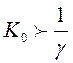, выполненное на рис.4.18. Используем диаграммы этого рисунка для обсуждения деталей процесса переключения триггера.

ОУ являются многокаскадными схемами, и их переходную характеристику, как показано в 2.2.6, можно моделировать ступенчатой функцией с определённой задержкой . Тогда на рис.4.18 при случайном увеличении напряжения , например, до ,    напряжение на выходе достигает величины  за интервал времени . Новое значение  по цепи обратной связи, которая предполагается  безынерционной,  изменяет напряжение на входе до величины . Таким образом, представление о задержке во времени оказывается необходимым условием для исключения неоднозначности определения напряжения на входе цепи с замкнутой обратной связью.  Новое значение  приводит к изменению (с задержкой )  выходного напряжения до   и т.д.  до перехода системы в точку «2». Следовательно, точка равновесия «0» является неустойчивой: малое начальное возмущение уводит систему из этой точки. Из расходящихся диаграмм рис.4.18 видно, что шаги между точками отсчёта по оси   возрастают. Поскольку расстояние между шагами по времени  одинаково, это показывает, что процесс является регенеративным, т.е. идёт с нарастающей скоростью, как и было показано в 4.4.