Импульсные устройства. Электронные триггеры, страница 10

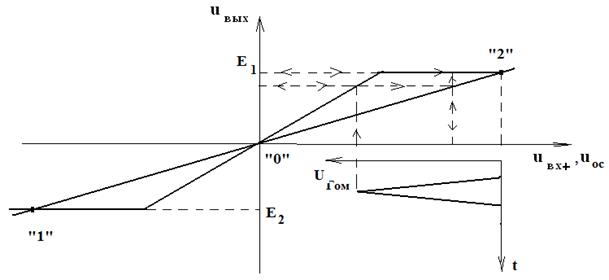
Рис. 4.19

В отличие от точки «0» равновесие системы в точках «1» и «2» является устойчивым. На рис.4.19 показано действие отрицательного импульса помехи на триггер в состоянии «2».  Для этого примера, если импульс помехи окончился,  система после двух переходов возвращается в исходное состояние. Рассмотренное свойство определяет помехоустойчивость триггера. Если на рис.4.19 импульс помехи переведёт  в область отрицательных значений, последовательные переходы переведут триггер в точку «1». Это обосновывает применение к точкам «1» , «2» термина «устойчивые в малом», т.е. до величины помехи, меньшей, чем  в точке «2».  С другой стороны,  диаграммы  рис.4.19 определяют требования к воздействиям, необходимым для функционально надёжного переключения триггера. 

Пусковая характеристика триггера на операционном усилителе

Для использования схемы рис.4.16 в качестве триггера удобен инверсный вход .  Изменение напряжения на этом дифференциальном входе ОУ смещает нулевую точку зависимости  , как показано на рис.4.20.  На этом рисунке с учётом реально большого коэффициента усиления ОУ  использована ступенчатая (релейная) характеристика.            

При малой величине   сохраняется устойчивое равновесие в точке «2». При превышении  порогового значения   исчезает пересечение характеристик и, следовательно,  исчезает решение уравнения (4.12) в точке «2». Используя подход, применённый на рис.4.18, 4.19, определяем, что  становится меньше необходимого для равновесия, в результате напряжение обратной связи около точки «2» уменьшается, что приводит к развитию регенеративного процесса уменьшения напряжения  вплоть  до перехода системы в точку «1».  Аналогично,  для вывода  триггера из точки «1» следует уменьшить напряжение инверсного входа до .

С использованием диаграмм рис.4.20 определяем

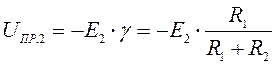 ,    (4.13)

Для иллюстрации свойств триггера удобно использовать диаграмму рис.4.21, которая называется пусковой характеристикой триггера. Предположим, что при   триггер  находится в точке «2», тогда выходное напряжение равно  (точка 0 на  рис.4.21). Увеличение  вначале изображается движением по горизонтальной ветви диаграммы без изменения . При достижении   (точка 1)  триггер регенеративно переходит в состояние  (точка 2)  при сохранении величины . Отметим, что вертикальный ход диаграммы па этом участке не связан с релейной аппроксимацией характеристики ОУ (рис.4.20), а представляет регенеративный процесс переключения триггера и время перехода между точками 1 и 2 есть время регенеративного процесса.  Если после этого возрастание  продолжается, то изображающая точка двигается вправо, но никаких  изменений  в состоянии триггера в соответствии с  рис.4.20  не происходит. Переход к уменьшению  приводит к обратному движению по горизонтальной ветви  при   без изменения состояния в точке 3, когда . При достижении отрицательного значения  (точка 4) триггер регенеративно возвращается в состояние  (точка 5).  Дальнейшее движение происходит по горизонтальной ветви, если  не достигнут порог . 

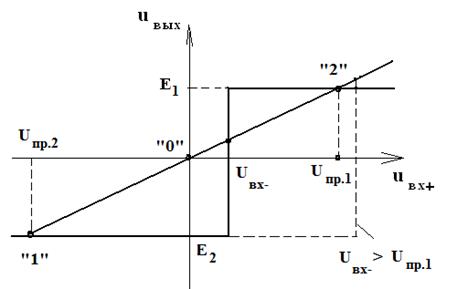
Рис. 4.20

Построение петли гистерезиса рис.4.21  является универсальным средством описания  триггеров с одним входом  как устройств памяти (сравните с рис.4.13).  Диаграммы определяют величину логического перепада , величину пороговых значений   и их разность – ширину петли гистерезиса.

Проведенный анализ позволяет также  оценить допустимую скорость изменения управляющего напряжения,  которая должна быть не слишком высокой, чтобы управляющий сигнал не изменился значительно за время переключения схемы.  Для  ОУ, содержащего несколько усилительных каскадов и  имеющего поэтому значительное время задержки, эти соотношения существенны.  В принципе, это подобно важному свойству ОУ как усилителя с отрицательной обратной связью, когда  ограничена максимальная скорость нарастания входного напряжения: нельзя увеличивать напряжение на входе раньше, чем «вернётся» напряжение обратной связи, поскольку при этом  не  вычтется  из напряжения на входе системы и входные каскады ОУ могут перейти в нелинейный режим насыщения или отсечки.