Составные части абстрактного автомата. Способы задания автоматов. Синхронные и асинхронные автоматы. Минимизация полностью определенного автомата. Структурная теория. Канонический метод структурного синтеза автомата. Кодирование состояний автомата. Гонки в автомате. Противогоночное кодирование состояний автомата

Составные части абстрактного автомата

 – входной алфавит (непустое множество попарно различных символов)

 - выходной алфавит

 - алфавит состояний (множество состояний)

 - начальное состояние

 и  задают однозначное отображение пар  и  в множество  и  и называются соответственно таблица переходов и таблица выходов

Автомат функционирует в дискретном времени, принимающем целые неотрицательные значения. В каждый момент времени  автомат находится в состоянии  (при ). В каждый момент времени автомат, находящийся в состоянии , способен воспринять входной сигнал  и выдавать соответствующий выходной сигнал , при этом он переходит в новое состояние . Смысл понятия автомата в реализации некоторого отображения  множества слов  в множество слов . Отображение осуществляется следующим образом. Каждое входное слово  последовательно подается на вход автомата, буква за буквой, предварительно установленного в . Последовательность входных сигналов вызывает появление однозначно определенной конечной последовательности , называемой выходным словом, соответствующим входному слову . Относя каждому входному слову  выходное слово , мы получаем . Таким образом мы ушли от времени .

Если  – конечны, то автомат конечен.  определены на всех парах , то автомат полностью определен. Иначе определен частично.

Два автомата с общими входным и выходным алфавитами называются эквивалентными, если они индуцируют одно и то же отображение множества слов входного алфавита в множество слов выходного алфавита. Автоматы, отличающиеся друг от друга лишь обозначением входных, выходных сигналов и состояний, называются изоморфными. Различают автоматы Мили (а) и Мура (б).

a)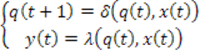 

b)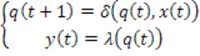 

Доказано, что для каждого автомата Мили существует эквивалентный автомат Мура и наоборот.

Способы задания автоматов

1)  табличный

Автомат задается двумя таблицами: переходов и выходов. Строки обоих таблиц соответствуют входным сигналам, а столбцы – состояниям.

таблица переходов автомата Мили

таблица выходов автомата Мили

Отмеченная таблица автомата Мура

2)  графический

Граф автомата – это ориентированный связный граф, вершины которого соответствуют состояниям, а дуги – переходам между ними.

3)  матричный

Матрица автомата – квадратная матрица , строки которой соответствуют исходным состояниям, а столбцы – состояниям перехода.

 - если сигналов несколько

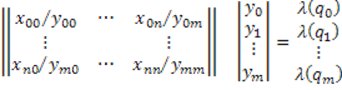
Для детерминированного автомата сохраняется условие однозначности переходов. В матрице входной сигнал может присутствовать не более одного раза.

Синхронные и асинхронные автоматы

Состояние  автомата называется устойчивым, если  выполняется . Автомат, у которого все состояния устойчивы, называется асинхронным. В противном случае автомат называется синхронным.

Минимизация полностью определенного автомата

Под минимизацией числа внутренних состояний автомата понимают процесс, целью которого является получение автомата, имеющего минимальное число внутренних состояний среди всех автоматов, реализующих требуемое отображение . Такой автомат называется минимальным автоматом.