Составные части абстрактного автомата. Способы задания автоматов. Синхронные и асинхронные автоматы. Минимизация полностью определенного автомата. Структурная теория. Канонический метод структурного синтеза автомата. Кодирование состояний автомата. Гонки в автомате. Противогоночное кодирование состояний автомата, страница 11

 

Комбинационная схема  осуществляет отображение множества внутренних состояний  исходного автомата на множество внутренних состояний автомата . Причем, это отображение разбивает все множество состояний исходного автомата на блоки разбиения  и каждому блоку разбиения соответствует вектор внутренних состояний  автомата . Разбиение определяется классом ошибок, подлежащих обнаружению. Модель обеспечивает обнаружение ошибок как в векторе выходов, так и в векторе состояний. Как и в предыдущем случае, ошибки обнаруживаются как в исходном автомате, так и в автомате .

 и

Не обнаруживаемые ошибки, которые в РО сохраняют значение сигнала на выходе . Кроме того, не обнаруживаются ошибки, которые приводят к изменению векторов  и  одновременно. Для реализации метода необходимо выполнить следующие задачи:

a.  выполнить разбиение  и , позволяющее обнаружить ошибки заданного класса

b.  построить автомат первая задача может быть не выполнима в ряде случаев. Достоинство – систему не надо переводить в особый режим. Недостаток – увеличение аппаратных средств. Уровень избыточности .

Использование специальных систем счисления и кодов

Система остаточных классов (СОК) – непозиционная система счисления, в которой любое число представляется в виде набора остатков от деления, представляемого или функционально связанного с ним числа, на фиксированные положительные числа , называемые основаниям СОК.

Все основания  являются простыми натуральными числами.

 – диапазон представляемых чисел

Изображаемое число  представляется в виде набора наименьших неотрицательных остатков от деления изображающего числа  на основание.

, если

, если

отдается положительным числам,  – отрицательным числам.

При таком способе представления число  изображается в виде остатков , где .

 называются разрядами представления числа в СОК.

В отличие от позиционной системы счисления в СОК арифметические операции выполняются раздельно по каждому основанию без переноса разрядов.

 

 

 

 

* - любая арифметическая операция

Недостатки СОК:

à человек не понимает, что за число

à невозможность сравнения чисел

à невозможность контроля переполнения разрядной сетки

Достоинство СОК - использование одного избыточного разряда позволяет выявлять сбои и отказы в любом разряде.

Коды Фибоначчи

Это ряд чисел, удовлетворяющих условию

 

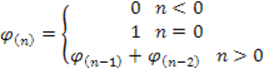
n – номер разряда

Обобщенный код Фибоначчи:

 

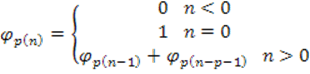
	0	1	2	3	4	5	6	7	8	9	10
0	1	2	4	8	16	32	64	128	256	512	1024
1	1	1	2	3	5	8	13	21	34	55	89
2	1	1	1	2	3	4	6	9	13	19	28
3	1	1	1	1	2	3	4	5	7	10	14

Особенность кода Фибоначчи при  - одно и то же число может иметь несколько представлений, которые получаются одно из другого. Но при заданном  и  существует единственное минимальное представление, в котором после каждого единичного разряда в сторону младших разрядов следует не менее  нулей. При  операция сложения может выполняться двумя способами:

A.  при сложении двух единичных разрядов возможен перенос в два предыдущих младших разряда ,

B.  при сложении двух единичных разрядов возможен перенос единицы в ,  одновременно

Достоинства:

  система позиционная

  легко определить факт переполнения

  легко выполнить операции сложения и умножения

  естественная избыточность ® возможность обнаружения ошибки

Недостаток – представление чисел больше  требует большего числа разрядов.