Другие предметы \ Проектирование цифровых устройств

Устройство умножения по модулю пять, страница 8

Существенные импликанты 3, 4, 6, 7. Они являются окончательным решением.

Функция :

1.  Нахождение простых импликант

Z1

Z2

Z4

0

*

*

0

1

*

*

1

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

*

Z6

 Z5

0

0

*

1

*

*

*

1

0

1

*

*

1

*

*

0

*

*

*

*

*

*

*

*

0

1

*

1

0

*

*

*

0

0

*

0

0

*

*

0

Z3

СКНФ:

 


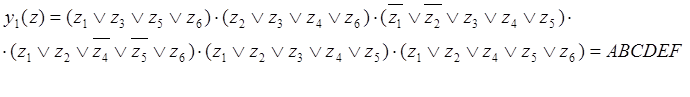СДНФ:

 


В результате преобразования СКНФ получаем СДНФ, которая покрывает все единичные и неопределённые наборы исходной.

1.  Построение таблицы покрытия

Простые импликанты

1

2

3

4

5

6

7

8

1

2

V

V

V

3

4

5

V

V

6

V

7

V

8

9

10

V

11

Существенные импликанты 2, 5, 6, 7, 10. Они являются окончательным решением.

В результате раздельной минимизации системы функций алгебры логики методом Кваина – Мак – Класки суммарная сложность системы составляет 37 операторов.

6)  Декомпозиция системы функций алгебры логики методом ПМФ

Декомпозиция функции У3.

Для синтеза воспользуемся декомпозиционной таблицей

Скачать файл