Устройство умножения по модулю пять, страница 15

Тип элемента	Обозначение	Максимальное время переключения	Ток потребления (при 0 сигнале на выходе)	Ток потребления (при 1 сигнале на выходе)
8И-НЕ	ЛА2	10 нс	40 мкА	4 мкА
4x2И-НЕ	ЛА3	8 нс	40 мкА	4 мкА
3x3И-НЕ	ЛА4	10 нс	40 мкА	4 мкА
2x4И-НЕ	ЛА1	10 нс	40 мкА	4 мкА
6НЕ	ЛН1	10 нс	40 мкА	4 мкА
4x2ИЛИ-НЕ	ЛЕ1	8 нс	40 мкА	4 мкА
3x3ИЛИ-НЕ	ЛЕ4	12 нс	40 мкА	4 мкА
2x4ИЛИ-НЕ	ЛЕ2	12 нс	40 мкА	4 мкА
Буф. элемент	ЛН9	10 нс	40 мкА	4 мкА

10) Факторизация системы логических уравнений

Факторизация логических уравнений, полученных методом минимизации.

Факторы имеющие качество 2: ,

Факторы имеющие качество 1:,, ,,

В результате система уравнений имеет вид:

Сложность полученного представления уменьшилась с 37 до 29 оператора И-ИЛИ-НЕ.

Дизъюнктивная факторизация системы логических уравнений, полученных методом приближающих монотонных функций.

Факторы имеющие качество 2:,

Сформируем множество дизъюнктивных факторов:

Проведём оценку их качества:

Фактор	Порождающее множество	Качество
	,	3
	,	3

Р результате получаем следующую систему уравнений:

{1}

{2,3}

{4}

{5,6}

{7}

{8,9,10}

{11,12}

{13,14}

Сформируем факторы выражения и определим их качество:

Фактор	Порождающее множество	Качество
Z1	+	0
Z2	+	0
Z3	+	0
Z4	+	0
Z5	+	0
Z6	+	0
Z2 Z5	+	2
Z2 Z3	+	1
Z2 Z6	+	0
Z3 Z5	+	0
Z2 Z4	+	0
Z3 Z6	+	0
Z1 Z6	+	0
Z3 Z4	+	0
Z1 Z5	+	0
Z1 Z4	+	0
Z5 Z6	+	1

Три фактора имеют качество больше 0, Причём факторизация может быть проведена с использованием всех трёх факторов одновременно. В результате получим следующую систему уравнений :

В результате система уравнений имеет вид:

Сложность полученного представления уменьшилась с 32 до 25 операторов И-ИЛИ-НЕ.

Так как базовым элементом в ИС КР1554 являются элементы И-НЕ, ИЛИ-НЕ, то они обладает более высоким быстродействием. Преобразуем логические уравнения с учётом данной элементной базы.

Для уравнений, полученных методом минимизации.

Максимальная глубина схемы реализующий данную систему уравнений =3, с учётом буферных элементов и блоков - реализующих связную реализацию системы сложность будет равной 6.

К сожалению, реализация данной системы уравнений только за счёт базовых элементов нерациональны, ввиду того что это приведёт к увеличению глубины схемы и как следствие к уменьшению быстродействия.

Для логических уравнений, полученных методом приближающих монотонных функций.

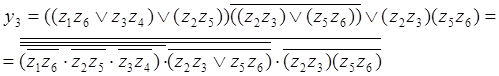
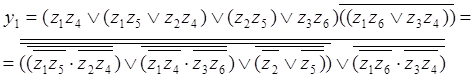
Максимальная глубина схемы реализующий данную систему уравнений =4, с учётом буферных элементов и блоков - реализующих связную реализацию системы сложность будет равной 7.

К сожалению, реализация данной системы уравнений только за счёт базовых элементов нерациональны, ввиду того что это приведёт к увеличению глубины схемы и как следствие к уменьшению быстродействия.

Так как для реализации с учётом элементной базы более предпочтительны системы преобразованные под элементы И-НЕ, ИЛИ-НЕ, при дальнейшем синтезе будем использовать эти системы.

11) Разработка принципиальной схемы синтезируемого устройства

Для выбора оптимальной схемы устройства сравним 2 полученные реализации:

·  Минимизация с последующим преобразованием под элементную базу

·  ПМФ с последующим преобразованием под элементную базу

Минимизация с последующим преобразованием под элементную базу

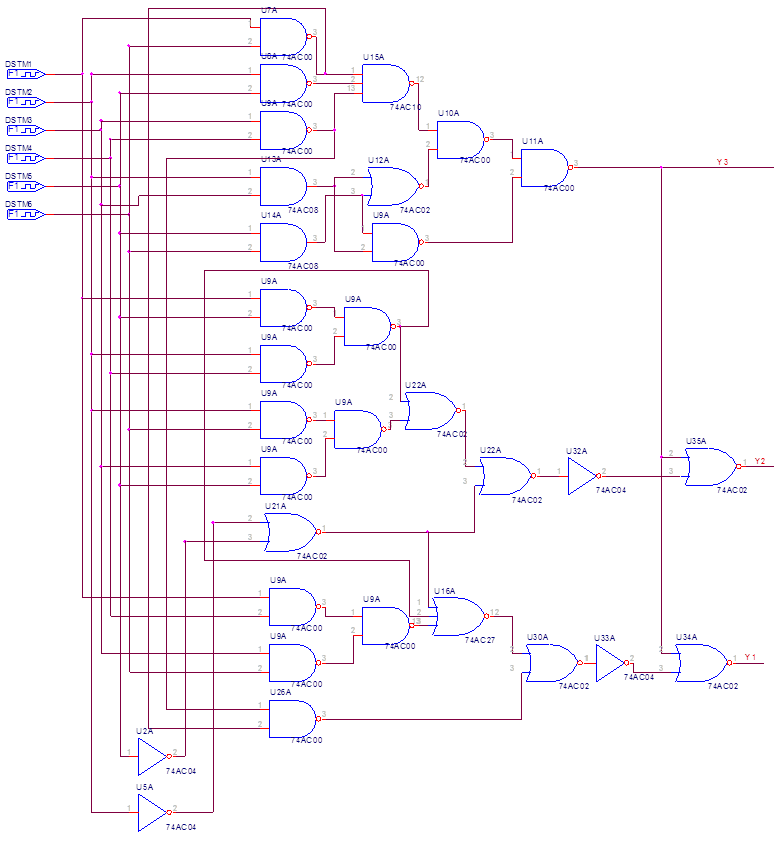
ПМФ с  последующим преобразованием под элементную базу

Схемы устройств содержат в базисе элементы: НЕ, И, ИЛИ-НЕ, И-НЕ