1.
Сформируем
выражение ![]() , оно совпадает с МДНФ функции.
, оно совпадает с МДНФ функции.
2. Для выражения
![]() формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
|
Фактор |
Порождающее множество |
Качество |
|
|
1,2,3 |
4 |
|
1 |
4,5,6 |
4 |
|
36 |
1,2,5,6 |
6 |
|
|
3,4,7 |
6 |
После факторизации получим следующее выражение для функции:
![]()
Сложность полученного представления в базисе И, ИЛИ, НЕ составляет 24 оператора.
Проведем
факторизацию функции ![]()
2.
Сформируем
выражение ![]() , оно совпадает с МДНФ функции.
, оно совпадает с МДНФ функции.
2. Для выражения
![]() формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
|
Фактор |
Порождающее множество |
Качество |
|
|
1,2 |
2 |
|
1 |
3,4 |
4 |
|
3 |
8,9 |
3 |
|
25 |
5,6,7 |
4 |
|
1245 |
6,7 |
5 |
|
14 |
6,7 |
2 |
После факторизации получим следующее выражение для функции:
![]()
Сложность полученного представления в базисе И, ИЛИ, НЕ составляет 21 оператор.
Проведем
факторизацию функции ![]()
3.
Сформируем
выражение ![]() , оно совпадает с МДНФ функции.
, оно совпадает с МДНФ функции.
2. Для выражения
![]() формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
|
Фактор |
Порождающее множество |
Качество |
|
25 |
1,2 |
2 |
|
14 |
3,4 |
2 |
|
|
5,6 |
4 |
|
|
7,9,11 |
4 |
|
|
8,10,12 |
4 |
После факторизации получим следующее выражение для функции:
![]() Сложность полученного представления в
базисе И, ИЛИ, НЕ составляет 42 оператора.
Сложность полученного представления в
базисе И, ИЛИ, НЕ составляет 42 оператора.
Проведем
факторизацию функции ![]()
4.
Сформируем
выражение ![]() , оно совпадает с МДНФ функции.
, оно совпадает с МДНФ функции.
2. Для выражения
![]() формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
формируем множество факторов, имеющих
наибольшее качество. Оно приведено в следующей таблице (в таблицу не включены
факторы, имеющие нулевое решение):
|
Фактор |
Порождающее множество |
Качество |
|
|
14,15 |
2 |
|
2356 |
1,2 |
4 |
|
|
11,13 |
2 |
|
|
6,7 |
2 |
|
|
8,9 |
2 |
|
|
10,12 |
2 |
|
14 |
3,4 |
4 |
|
14 |
3,4,5 |
4 |
После факторизации получим следующее выражение для функции:
![]()
Сложность полученного представления в базисе И, ИЛИ, НЕ составляет 28 оператор.
Таким образом в ходе факторизации получим систему уравнений:
![]()
![]()
![]()
![]()
При рассмотрении системы в целом можно выделить следующие дизъюнктивные и конъюнктивные факторы:
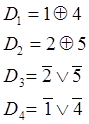
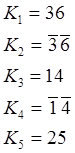
После факторизации система ФАЛ будет выглядеть следующим образом:
![]()
![]()
![]()
![]()
Сложность
системы функций с учетом сложности совместной реализации в базисе И, ИЛИ, НЕ
составляет ![]() операторов.
операторов.
Данное представление ФАЛ на 127 операторов меньше, чем системы ФАЛ, полученная методом минимизации.
7.2.Факторизация логических уравнений, полученных методом приближающих монотонных функций
Проведем факторизацию системы логических уравнений, полученных в результате декомпозиции методом ПМФ. Учитывая, что функции разложения монотонны, а количество возможных факторов невелико, факторизацию проведем сразу для всей системы функций разложения.
![]()
![]()
![]()
![]()
Первый цикл факторизации.
1. Сформируем
выражение ![]()
![]()
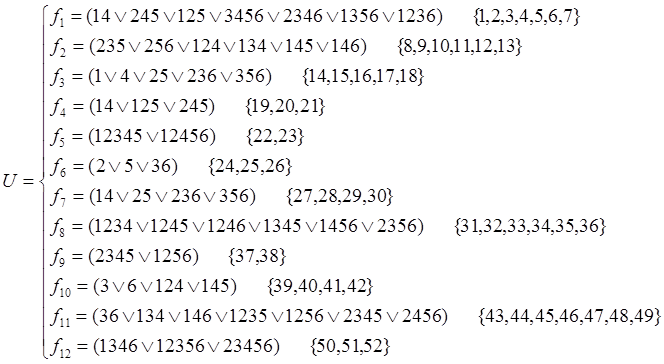
2. Проведем поиск дизъюнктивных факторов и сформируем их множество:
|
Фактор |
Качество |
|
14 25 134 124 |
6 6 4 4 |
3. Сформируем выражение
![]()
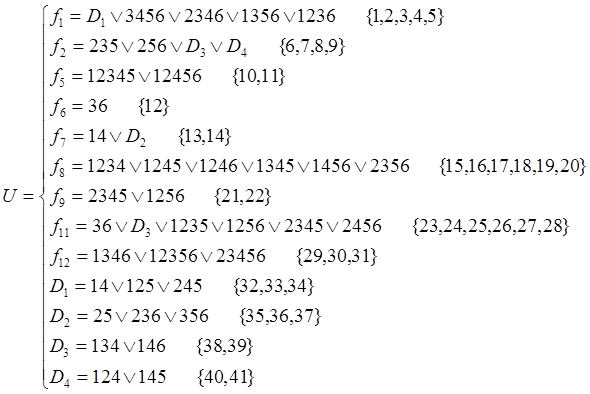
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.