Разработка устройства суммирования по модулю девять двух двоичных трехразрядных, страница 19

Первый цикл формирования ПМФ

1. .

2. Несущественные переменные отсутствуют, что следует из постановки задачи.

3. .

7. .

11. Подмножества  в декомпозиционной таблице разбиты на подмножества  по числу  неинверсных переменных в наборах и упорядочены в порядке убывания значения . Благодаря этому выполнение данной операции обеспечивается автоматически при использовании рассмотренной декомпозиционной таблицы.

12. Определяем  .

13. Сформируем ПМФ  и .

13.1. Сначала формируем ПМФ , характеристические наборы которой включают следующие наборы

13.2. Формируем подмножество

13.3. Поскольку , переходим к формированию ПМФ .

13.4. Формируем первичную ДНФ  ПМФ , удовлетворяющую условиям

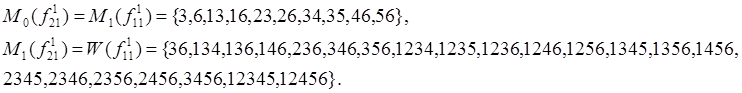
13.5. Принимаем

13.6.

13.7. Поскольку  то переходим к расширению первичной ДНФ ПМФ .

13.8. Формируем первичную ДНФ  удовлетворяющую условию:

13.9. Формируем подмножество . Значит, корректировка ПМФ  не требуется.

13.13. Корректируем первичную ДНФ ПМФ:

   

13.14.

Процесс формирования ПМФ  и  окончен. В результате его проведения получены следующие первичные ДНФ ПМФ:

14. Сокращаем характеристическое подмножество , исключая наборы, реализованные композицией сформированных ПМФ:

15. Поскольку  , необходим еще цикл декомпозиции.

16. , переходим к очередному циклу декомпозиции.

Второй цикл формирования ПМФ.

2. Несущественные переменные отсутствуют.

3.

4.

11. Подмножества  в декомпозиционной таблице разбиты на подмножества  по числу  неинверсных переменных в наборах и упорядочены в порядке убывания значения . Благодаря этому выполнение данной операции обеспечивается автоматически при использовании рассмотренной декомпозиционной таблицы.

12. Определяем  .

13. Сформируем ПМФ  и .

13.1. Сначала формируем ПМФ , характеристические наборы которой включают следующие наборы

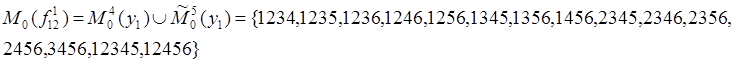
13.2. Формируем подмножество

13.3. Поскольку , ПМФ  не формируется.

14. Сокращаем характеристическое подмножество , исключая наборы, реализованные композицией сформированных ПМФ:

15. Поскольку   процесс декомпозиции окончен.

17. Оптимизируем ПМФ .

Поскольку число импликант в первичной ДНФ ПМФ  невелико, используем второй способ формирования множества простых импликант.

Поскольку первичная ДНФ ПМФ содержит элементарные конъюнкции 4, 5-го рангов, ее оптимизация возможна за счет элементарных конъюнкций четвертого и меньшего рангов.

Сначала рассмотрим конъюнкции 5-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Рассмотрим конъюнкции 4-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Таким образом, полученная ДНФ ПМФ является оптимальной:

18. 

17. Оптимизируем ПМФ .

Поскольку число импликант в первичной ДНФ ПМФ  невелико, используем второй способ формирования множества простых импликант.

Поскольку первичная ДНФ ПМФ содержит элементарные конъюнкции 2, 3 и 4-го рангов, ее оптимизация возможна за счет элементарных конъюнкций третьего и меньшего рангов.

Сначала рассмотрим конъюнкции 4-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Рассмотрим конъюнкции 3-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Таким образом, исходная функция является оптимальной ДНФ ПМФ:

18.

17. Оптимизируем ПМФ .

Поскольку число импликант в первичной ДНФ ПМФ  невелико, используем второй способ формирования множества простых импликант.

Поскольку первичная ДНФ ПМФ содержит элементарные конъюнкции 1-го и 3-го рангов, ее оптимизация возможна за счет элементарных конъюнкций второго и меньшего рангов.

Сначала рассмотрим конъюнкции 3-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :