Другие предметы \ Проектирование цифровых устройств

Разработка устройства суммирования по модулю девять двух двоичных трехразрядных, страница 18

Сначала рассмотрим конъюнкции 4-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Рассмотрим конъюнкции 3-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Найдем оптимальное покрытие импликант первичной ДНФ. Для этого воспользуемся таблицей покрытия.

25

124

145

236

356

1346

236

+

356

+

25

+

14

+

+

+

13

+

34

+

16

+

46

+

Таким образом, получаем следующую оптимальную ДНФ ПМФ:

17. Оптимизируем ПМФ .

Поскольку число импликант в первичной ДНФ ПМФ  невелико, используем второй способ формирования множества простых импликант.

Поскольку первичная ДНФ ПМФ содержит элементарные конъюнкции 2-го и 1-го рангов, ее оптимизация возможна за счет элементарных конъюнкций первого.

Сначала рассмотрим конъюнкции 2-го ранга:

Исключаем те наборы, которые реализуют наборы нулевого характеристического подмножества :

Таким образом, полученная ДНФ ПМФ оптимальная:

18.

Процесс оптимизации окончен.

Получаем следующее представление ФАЛ :

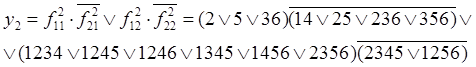
Сложность данного представления ФАЛ в базисе И, ИЛИ, НЕ составляет  оператор, что на 22 оператора меньше, чем при методе минимизации.

Рассмотрим процесс формирования декомпозиции функции

Воспользуемся декомпозиционной таблицей:

Входной код

Входной код

Выходной код

ПМФ

ОДНФ

1

2

3

4

5

6

7

8

9

123

456

1

V

V

V

V

V

V

123

123

123

12-

1-3

-23

45-

4-6

-56

456

456

456

0

1

1

0

1

1

V

V

V

V

V

V

V

V

V

V

V

V

V

1

V

1

V

V

V

V

V

V

V

V

V

V

V

V

V

1

V

1

123

123

123

12-

12-

12-

1-3

1-3

1-3

1--

-23

-23

-23

-2-

--3

4--

-5-

--6

45-

4-6

-56

45-

4-6

-56

456

45-

4-6

-56

456

456

0

0

0

1

0

0

0

1

0

0

0

0

0

0

0

V

V

V

V

V

V

V

V

V

V

V

V

V

V

V

V

1

V

V

1

V

V

V

V

1

V

V

1

V

1

V

V

V

V

V

V

V

V

V

V

V

V

V

V

V

V

1

V

V

1

V

V

V

V

1

V

V

1

V

1

123

12-

12-

12-

1-3

1-3

1-3

1--

1--

1--

-23

-23

-23

-2-

-2-

-2-

--3

--3

--3

---

---

4--

-5-

--6

4--

-5-

--6

45-

4-6

-56

4--

-5-

--6

45-

4-6

-56

45-

4-6

-56

456

1

1

0

1

0

1

0

1

0

1

1

1

0

0

1

1

1

0

0

1

V

1

V

V

V

V

1

V

V

V

V

V

V

V

V

V

V

V

1

V

1

V

V

V

V

1

V

V

V

V

1

V

V

V

V

V

V

V

V

V

V

V

1

V

1

V

V

V

12-

1-3

1--

1--

1--

-23

-2-

-2-

-2-

--3

--3

--3

---

---

---

---

---

4--

-5-

--6

---

4--

-5-

--6

4--

-5-

--6

45-

4-6

-56

0

1

0

0

1

1

0

0

1

1

1

0

0

1

1

V

V

V

V

V

V

V

V

V

1

V

V

V

V

V

V

V

V

V

1

1--

-2-

--3

---

---

---

---

---

---

4--

-5-

--6

0

0

1

0

0

1

1

1

1

1
Скачать файл