Кинематическое и динамическое исследование рычажного механизма пресса. Конструкторская разработка редуктора и расчёт прочности отдельных деталей привода пресса, страница 5

Скорости точек Р, a,dи других равны нулю. Поэтому на плане скоростей (см. лист 1 курсового проекта) Р, a, d некоторые другие находятся в одной точке.

По принципу векторных уравнений составляем для заданного механизма векторные уравнения скоростей точек звеньев. Построение планов скоростей начинаем с точки Р, затем откладываем вектор Рb, перпендикулярно звену AB. Далее, находим скорость точки C. Для этого составим уравнения, которые решим графическим методом:

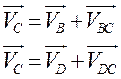
Модуль и направление скорости точки B известны, скорость точки A равна нулю. На чертеже из конца вектора a проведем прямую, перпендикулярную звену АВ и еще одну прямую из точки Dперпендикулярную звену CD. Затем, проводим прямую с конца вектора b параллельную звену BC. На пересечении этой прямой с перпендикуляром получим точку, соединив которую с полюсом Р находим скорость точки C по направлению и по модулю, умножив на масштабный коэффициент.

Найти вектор ed можно из теоремы подобия по формуле:

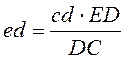
Модуль и направление скорости точки E  найдем, умножив на масштабный коэффициент, скорость точки D равна нулю. На чертеже из конца вектора d проведем вектор de, направленный по вектору dc. Далее, из конца вектора e проводим прямую перпендикулярную звену EF и на пересечении её с вертикальной осью, вдоль которой совершает ползун возвратно – поступательные движения, найдём точку, соединив которую с полюсом, найдём модуль и направление скорости f, умножив длину вектора Рf на чертеже на масштабный коэффициент.

Таким образом, получили замкнутый многоугольник векторов скоростей точек звеньев механизма. Аналогичные построения делаем для каждого положения механизма.

Соединив концы векторов для каждого положения механизма, получим годограф скоростей точки b, который представляет собой окружность радиусом Рb. Аналогично строим годографы для точек C, E, F. Построенные планы скоростей позволяют определить направление и величину угловой скорости любого звена механизма

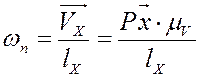
План скоростей дает возможность находить касательные к траекториям точек механизма, не выстраивая этих траекторий.

1.2.3 Построение планов ускорений механизма

Последовательность построения планов ускорений та же самая, по тем же подходам, что и план скоростей. Полюс плана ускорений обозначается П. Масштабный коэффициент плана ускорений, находится:

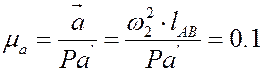
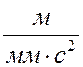
Рассмотрим построение планов ускорения на примере первого положения механизма (см. лист 1 курсового проекта). Ускорения точек A, D равны нулю,  значит точки  a’, d’ совпадают с  полюсом П. Для нахождения ускорения точки C, составим систему уравнений, которые решим графически:

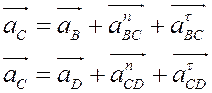
Ускорения точек Bи D известны. Модуль ускорений найдем по формуле:

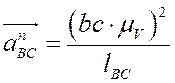
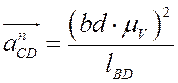
Ускорение  направлено параллельно звену BC от точки B к точке C,а ускорение направлено параллельно звену DCот точки Cк точке DТангенциальные ускорения и  известны только по направлению, они направлены перпендикулярно соответственно звеньям BCи DC. Начинаем построения: от ускорения  откладываем  и от ускорения  откладываем , далее с концов векторов  и проводим линии направлений векторов и .На пересечении линий получим точку c’,соединив которую с полюсом  П , получим ускорение точки  C.

Найти ускорение точки Eможно из теоремы подобия с учётом того, что ускорение точки C иE сонаправленно. Решив следующее уравнение, найдём модуль и направление точки E, умножив значение на масштабный коэффициент:

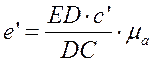
Ускорения точки Fнайдём из суммы векторов:

На плане положений из конца вектора e’ проводим прямую перпендикулярную звену EF и на пересечении её с вертикальной осью, вдоль которой перемещается ползун, найдём точку, соединив которую с полюсом, получим ускорение точки F. Действительное ускорение точки F получим, умножив на масштабный коэффициент:

Чтобы определить направление углового ускорения звена, например, звена 4, надо вектор перенести в точку C механизма. Угловое ускорение будет направлено в сторону .
2. ПРИВОД

Схема редуктора

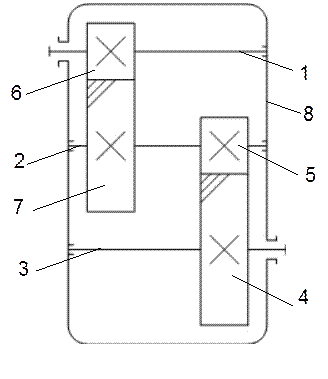
Рис. 2

1 – вал быстроходной ступени