Для нахождения направления ![]() воспользуемся диаграммой
сил полезного сопротивления (см. задание на
курсовой проект), где указано направление силы полезного сопротивления. Сила полезного сопротивления направлена противоположно движению выходного звена 6, причем
на диаграмме также указано крайнее
положение точки F.
Отсюда делаем вывод, что в заданном механизме направление
рабочего хода с верху вниз. Для выбора направления
воспользуемся диаграммой
сил полезного сопротивления (см. задание на
курсовой проект), где указано направление силы полезного сопротивления. Сила полезного сопротивления направлена противоположно движению выходного звена 6, причем
на диаграмме также указано крайнее
положение точки F.
Отсюда делаем вывод, что в заданном механизме направление
рабочего хода с верху вниз. Для выбора направления ![]() необходимо на плане
положений двигаться от одного крайнего положения кривошипа к другому таким образом, чтобы выходное звено совершало бы движение в направлении стрелки рабочего хода.
необходимо на плане
положений двигаться от одного крайнего положения кривошипа к другому таким образом, чтобы выходное звено совершало бы движение в направлении стрелки рабочего хода.
На чертеже видно, что рабочий ход звено
6 совершает из положения 0 в положение 6, а затем возвращается от
шестого положения в двенадцатое положение, совпадающее с
нулевым положением, при этом ![]()
Из центра вращения кривошипа, точки A, проведем окружность радиусом AB,
затем разобьем ее на двенадцать равных частей точками. Соединим эти точки с точкой A,
получим двенадцать положений входного звена 2 механизма. Далее для
выбранного положения звена 2 из точки B
проведем дугу радиусом, равным длине BC звена 3. Из точки Dпроведем дугу радиусом равным длине DC звена 4. В пересечениях этих дуг и лежит точка C, определяющая положение звеньев 3 и 4.
Положение точки F найдем таким же образом,
проведя одну дугу из точки E
равную длине звена EF .
На пересечении этой дуги с вертикальной осью, вдоль которой
перемещается ползун, и есть положение точки F.
Таким образом, проделывая аналогичные операции для каждого
положения входного звена 2, можно построить все остальные планы. Нумеруются положения
звеньев в направление угловой скорости ![]() входного звена.
входного звена.
После построения планов положений переходят к построению планов скоростей.
1.2.2 Построение планов скоростей механизма
Данное построение производится на основе планов положений механизма и векторных уравнений, в результате решения которых определяются линейные скорости точек звеньев, а затем угловые скорости звеньев механизма, как по модулю, так и по направлению.
Планом скоростей называется масштабное графическое изображение, соответствующее заданному положению исследуемого механизма, и представляет собой векторный многоугольник (замкнутый), на котором имеется единая для всех векторов точка отсчета Р, называемая полюсом плана скоростей.
Вектора, выходящие из полюса, представляют собой абсолютные значения скоростей точек звеньев механизма, а вектора, соединяющие концы первых, то есть абсолютных скоростей, есть линейные относительные скорости точек звеньев механизма. Эти векторы направлены к той точке, которая стоит первой в индексе скорости.
На план скоростей, как и на план ускорений в дальнейшем, распространяется теорема подобия: отрезки, образованные точками звеньев на плане механизма, подобны и сходственно расположены по отношению к отрезкам на плане скоростей. Для построения планов скоростей используется теорема о сложении движений: абсолютного и относительного.
Если звено вращается вокруг точки, то линейная скорость будет направлена перпендикулярно звену в сторону его угловой скорости.
Построение плана скоростей является масштабным, то есть, измерив, расстояние от полюса до точки, скорость которой требуется найти, и, умножив его на масштабный коэффициент, получим реальную скорость.
Для построения плана скоростей вычислим
масштабный коэффициент - отношение действительной величины скорости к
длине отрезка на чертеже. Масштабный коэффициент планов скоростей
обозначается ![]()
Скорость точки B по
принципу векторных уравнений равна сумме скоростей точки A и звена AB. Но
так как точка A не совершает движения, то
ее скорость равна нулю. Поэтому модуль скорости точки B равен лишь скорости звена AB, то
есть определяется
как произведение угловой скорости ![]() на длину звена.
на длину звена.
Угловую скорость кривошипа определим по формуле:
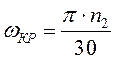 ;
;
![]() м/с
м/с
Масштабный коэффициент:
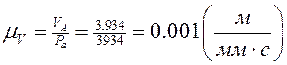
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.