данной балки,
используя условие прочности при изгибе, определим величину момента
сопротивления сечения ![]() :
:
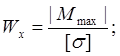
![]()
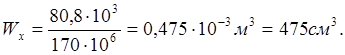
А так же определим площадь поперечного сечения для случаев:
а) Двутавр. Из
таблиц сортамента прокатной стали (ГОСТ 8239-89) определяем номер двутавра - №30;
![]() площадь поперечного сечения
площадь поперечного сечения ![]()
Так как момент сопротивления принятого двутавра меньше чем расчетный, то необходимо определить перенапряжение, которое не должно превышать 5%.
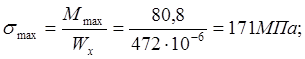
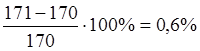 , что допустимо.
, что допустимо.
б) Сдвоенный
швеллер. Момент сопротивления одного швеллера ![]() . Из
таблиц сортамента прокатной стали (ГОСТ 8240-89) определяем номер одного
швеллера - №24;
. Из
таблиц сортамента прокатной стали (ГОСТ 8240-89) определяем номер одного
швеллера - №24; ![]() площадь поперечного сечения
площадь поперечного сечения ![]() , следовательно, площадь поперечного
сечения сдвоенного швеллера равна
, следовательно, площадь поперечного
сечения сдвоенного швеллера равна ![]()
в) Круг.
![]()
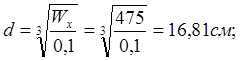
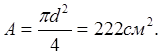
г)
Прямоугольник, ![]() :
:
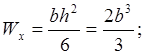
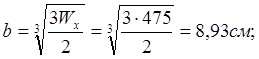
![]()
![]()
Приняв площадь
двутавра за единицу, получаем соотношение площадей ![]() .
Наиболее рациональным является двутавровое поперечное сечение.
.
Наиболее рациональным является двутавровое поперечное сечение.
3. Построение эпюр нормальных и касательных напряжений для двутаврового поперечного сечения.
Нормальные
напряжения вычисляем по формуле Навье 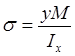 .
.
В опасном
сечении ![]() ,
, ![]()
Данные для
двутавра №30: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обозначим характерные точки по высоте сечения (рисунок 6).
Точка 1,5:
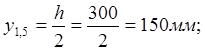
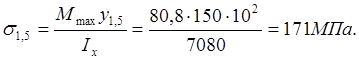
Точка 2,4:
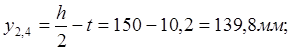
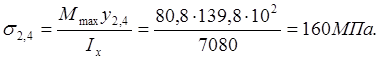
Точка 3:
![]() т.к.
т.к. ![]() .
.
Касательные
напряжения вычисляем по формуле 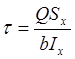 .
.
В точках 1 и 5 ![]() .
.
В точках 2 и 4
![]() изменяется скачкообразно, за счет
изменения ширины волокна, проходящего через точку 2. График в этих точках носит
несколько условный характер, так как резкое изменение ширины сечения вызывает
местное распределение напряжений. Знак касательных напряжений тот же, что и
поперечной силы
изменяется скачкообразно, за счет
изменения ширины волокна, проходящего через точку 2. График в этих точках носит
несколько условный характер, так как резкое изменение ширины сечения вызывает
местное распределение напряжений. Знак касательных напряжений тот же, что и
поперечной силы ![]() .
.
Точки 2 и 4. Вычисляем статический момент площади поперечного сечения:
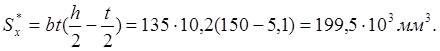
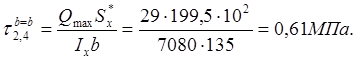
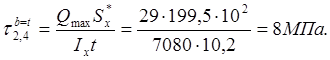
Точка 3. ![]() .
.
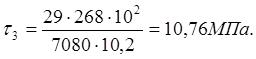
Строим эпюры напряжений (рисунок 6).
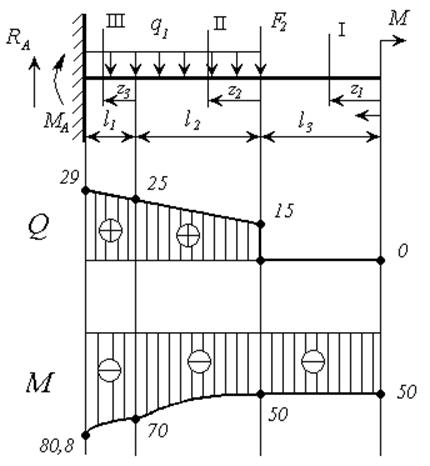
Рисунок 5
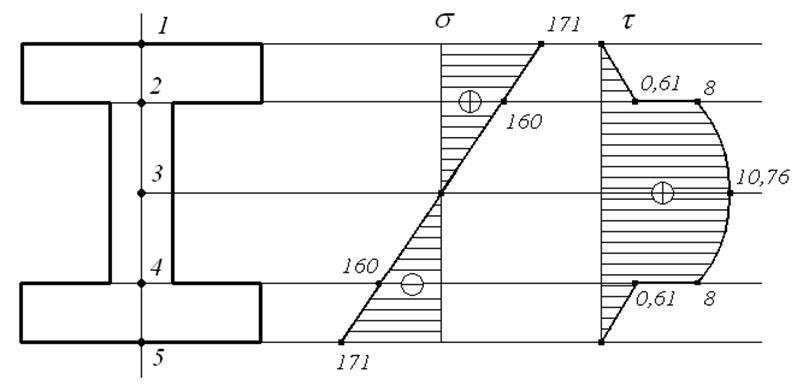
Рисунок 6
Решение задачи №2
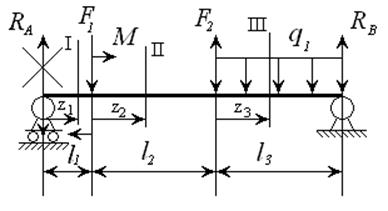
Рисунок 7
Для двух опорной балки рисунок 7 определим опорные реакции.
![]()
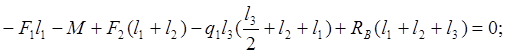
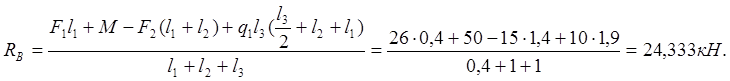
![]()
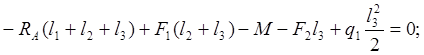
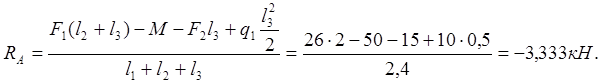
![]()
![]()
![]()
1. Для
определения поперечной силы ![]() и изгибающего момента
и изгибающего момента ![]() воспользуемся методом сечений.
воспользуемся методом сечений.
Участок I, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Участок II, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Участок III, ![]()
![]()
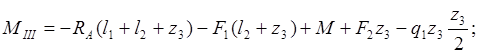
![]()
![]()
![]()
![]()
![]()
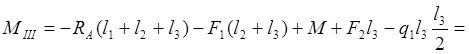
![]()
По полученным
данным строим эпюры поперечной силы ![]() и изгибающего момента
и изгибающего момента ![]() (рисунок 8).
(рисунок 8).
2. Для данной
балки, используя условие прочности при изгибе, определим величину момента
сопротивления сечения ![]() :
:
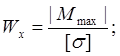
![]()
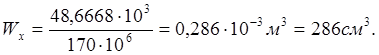
А так же определим площадь поперечного сечения для случаев:
а) Двутавр. Из
таблиц сортамента прокатной стали (ГОСТ 8239-89) определяем номер двутавра -
№24; ![]() площадь поперечного сечения
площадь поперечного сечения ![]()
б) Сдвоенный
швеллер. Момент сопротивления одного швеллера ![]() . Из
таблиц сортамента прокатной стали (ГОСТ 8240-89) определяем номер одного
швеллера - №20;
. Из
таблиц сортамента прокатной стали (ГОСТ 8240-89) определяем номер одного
швеллера - №20; ![]() площадь поперечного сечения
площадь поперечного сечения ![]() , следовательно, площадь поперечного
сечения сдвоенного швеллера равна
, следовательно, площадь поперечного
сечения сдвоенного швеллера равна ![]()
в) Круг.
![]()
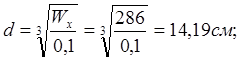
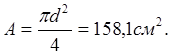
г)
Прямоугольник, ![]() :
:
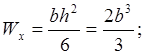
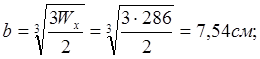
![]()
![]()
Приняв площадь
двутавра за единицу, получаем соотношение площадей ![]() .
Наиболее рациональным является двутавровое поперечное сечение.
.
Наиболее рациональным является двутавровое поперечное сечение.
3. Построение эпюр нормальных и касательных напряжений для двутаврового поперечного сечения.
Нормальные
напряжения вычисляем по формуле Навье 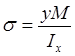 .
.
В опасном
сечении ![]() ,
, ![]()
Данные для
двутавра №24: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обозначим характерные точки по высоте сечения (рисунок 9).
Точка 1,5:
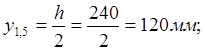
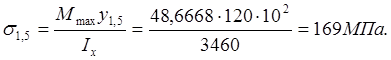
Точка 2,4:
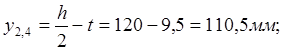
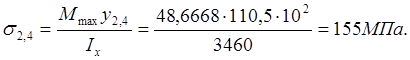
Точка 3:
![]() т.к.
т.к. ![]() .
.
Касательные
напряжения вычисляем по формуле 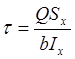 .
.
В точках 1 и 5 ![]() .
.
В точках 2 и 4
![]() изменяется скачкообразно, за счет
изменения ширины волокна, проходящего через точку 2. График в этих точках носит
несколько условный характер, так как резкое изменение ширины сечения вызывает
местное распределение напряжений. Знак касательных напряжений тот же, что и
поперечной силы
изменяется скачкообразно, за счет
изменения ширины волокна, проходящего через точку 2. График в этих точках носит
несколько условный характер, так как резкое изменение ширины сечения вызывает
местное распределение напряжений. Знак касательных напряжений тот же, что и
поперечной силы ![]() .
.
Точки 2 и 4. Вычисляем статический момент площади поперечного сечения:
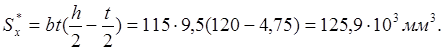
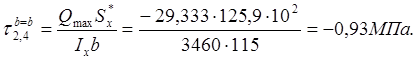
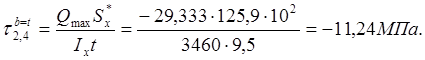
Точка 3. ![]() .
.
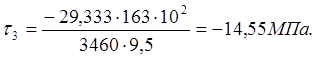
Строим эпюры напряжений (рисунок 9).
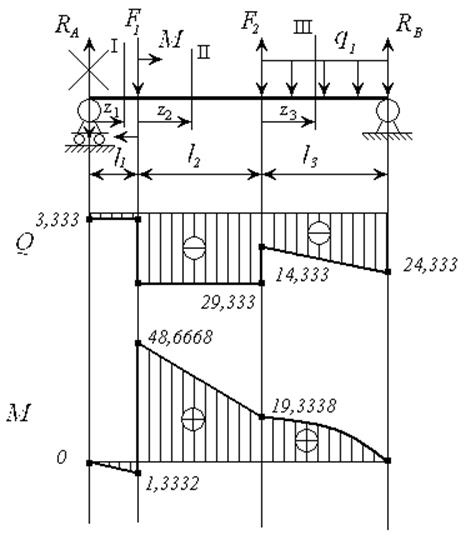
Рисунок 8
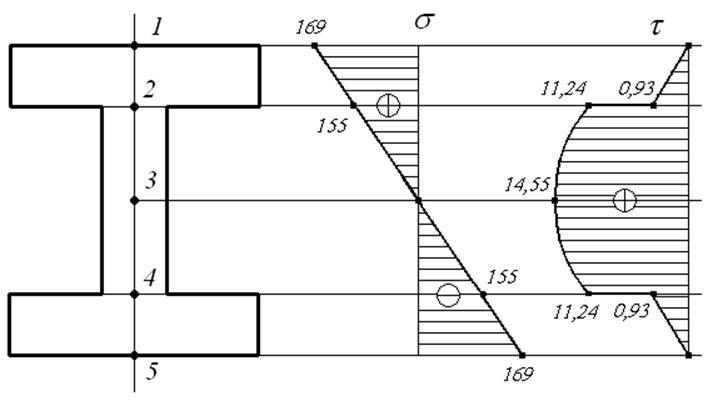
Рисунок 9
Решение задачи №3
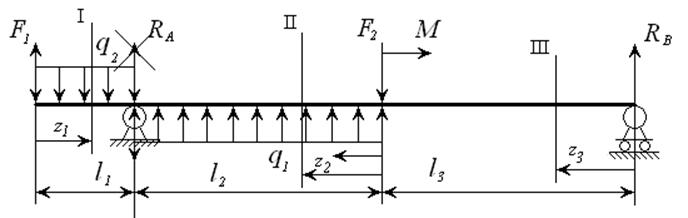
Рисунок 10
Для балки двух опорной с консолью рисунок 10 определим опорные реакции.
![]()
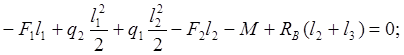
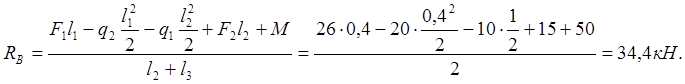
![]()
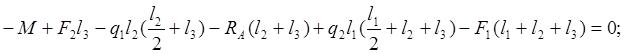
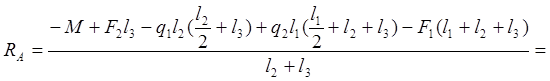
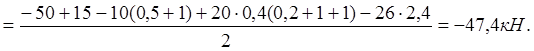
![]()
![]()
![]()
1. Для
определения поперечной силы ![]() и изгибающего момента
и изгибающего момента ![]() воспользуемся методом сечений.
воспользуемся методом сечений.
Участок I, ![]()
![]()
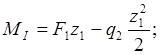
![]()
![]()
![]()
![]()
![]()
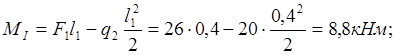
Участок III, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Участок II, ![]()
![]()
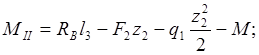
![]()
![]()
![]()
![]()
![]()
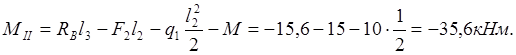
По полученным
данным строим эпюры поперечной силы ![]() и изгибающего момента
и изгибающего момента ![]() (рисунок 11).
(рисунок 11).
2. Для данной
балки, используя условие прочности при изгибе, определим величину момента
сопротивления сечения ![]() :
:
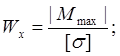
![]()
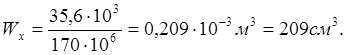
А так же определим площадь поперечного сечения для случаев:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.