Контрольная работа №4. Показательные и логарифмические уравнения, неравенства, системы. Производная
Часть I
(Записать краткое решение и номер полученного ответа)
A1. Найти значение выражения ![]() .
.
1) 19 2) 5 3) 5,4 4) 12
A2. Найти значение ![]() , если
, если ![]() .
.
1) 0,25 2) 9 3) 81 4) 243
A3. Найти множество значений функции 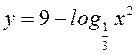 .
.
1)
![]() 2)
2) ![]() 3)
3)
![]() 4)
4) ![]()
A4. Указать число целых корней уравнения ![]() .
.
1) 5 2) 7 3) 9 4) 10
A5. Найти производную функции ![]() .
.
1)
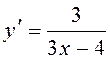 2)
2) 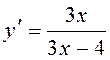 3)
3)
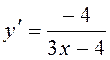 4)
4) ![]()
A6. Найти значение производной функции ![]() в точке
в точке ![]() .
.
1) 1 2) 2 3) 3 4) 4
A7. Найти угловой коэффициент касательной к графику функции
![]() в точке с абсциссой
в точке с абсциссой ![]()
![]() .
.
1)
![]() 2)
2) 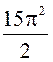 3)
–5 4) 15
3)
–5 4) 15
A8. Найти сумму целых чисел, лежащих на промежутке ![]() и входящих в область определения функции
и входящих в область определения функции ![]() .
.
1) 15 2) 12 3) 10 4) 9
A9. Найти множество значений функции ![]() .
.
1)
![]() 2)
2) ![]() 3)
3)
![]() 4)
4) ![]()
A10. Решить неравенство 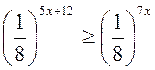 .
.
1)
![]() 2)
2) ![]() 3)
3)
![]() 4)
4) ![]()
Часть II
(Записать полное решение и полученный ответ)
Найти значение выражения:
B1. ![]() .
.
B2. 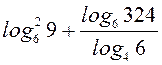 .
.
B3. Вычислить 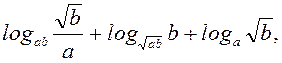 если известно, что
если известно, что ![]() .
.
B4. Найти наименьшее значение функции 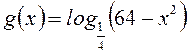 .
.
B5. Найти область определения функции ![]() .
.
B6. Найти сумму корней уравнения 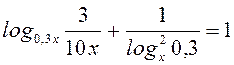 .
.
B7. Найти сумму всех целых чисел, входящих в область
определения функции ![]() .
.
B8. Найти значение выражения 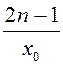 , если n
– число корней уравнения
, если n
– число корней уравнения ![]() , а x0 – его
положительный корень.
, а x0 – его
положительный корень.
B9. Вычислить ![]() , если
, если ![]() – меньший корень уравнения
– меньший корень уравнения ![]() , кратный 8.
, кратный 8.
B10. Решить уравнение 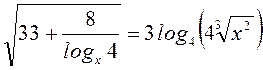 .
.
B11. Найти сумму корней уравнения ![]()
B12. Решить уравнение ![]()
B13. Найти все значения а, при которых уравнение ![]() имеет ровно один корень.
имеет ровно один корень.
Решить неравенства:
B14. 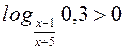 .
.
B15. ![]()
B16. ![]()
B17. Найти число целых решений неравенства ![]() .
.
B18. Найти количество целых решений неравенства ![]()
B19. Вычислить значение производной функции 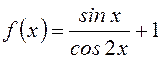 в точке
в точке 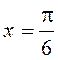 .
.
B20. Найти значение выражения m + 2M, если m и M
– значения функции 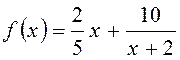 в точках минимума и максимума
соответственно.
в точках минимума и максимума
соответственно.
B21. Через точку ![]() проходят
две касательные к графику функции
проходят
две касательные к графику функции ![]() Найти сумму абсцисс
точек касания.
Найти сумму абсцисс
точек касания.
B22. К графику функции 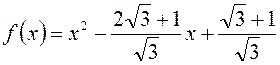 в
точке с абсциссой
в
точке с абсциссой 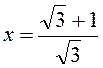 проведена касательная. Найти
угол между частью касательной, лежащей в верхней полуплоскости
проведена касательная. Найти
угол между частью касательной, лежащей в верхней полуплоскости ![]() и положительным направлением оси Oх.
и положительным направлением оси Oх.
B23. Касательная к графику функции ![]() перпендикулярна
прямой
перпендикулярна
прямой ![]() . Найти координаты точки касания.
. Найти координаты точки касания.
B24. Производная функции f![]() имеет вид
имеет вид ![]() Найти число точек
экстремума функции
Найти число точек
экстремума функции ![]() .
.
B25. Найти значение 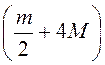 , если
m и M – соответственно наименьшее и наибольшее значения
функции
, если
m и M – соответственно наименьшее и наибольшее значения
функции 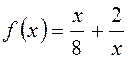 на отрезке
на отрезке ![]() .
.
Часть III
(Записать подробное решение и полученный ответ)
C1. Решить
систему уравнений 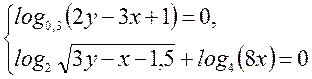 .
.
C2. При каких значениях параметра с сумма
логарифмов ![]() и
и ![]() будет
меньше единицы при всех допустимых значениях х?
будет
меньше единицы при всех допустимых значениях х?
C3. Найти все значения с, при которых области определения функций
![]() и
и 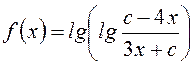 пересекаются
между собой.
пересекаются
между собой.
C4. Найти все значения k, при
каждом из которых наибольшее из двух чисел ![]() и
и ![]() меньше 9.
меньше 9.
C5. Даны два уравнения: ![]() и
и 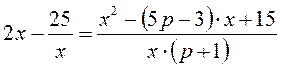 . Значение параметра р выбирается
так, что
. Значение параметра р выбирается
так, что ![]() , и число различных корней первого
уравнения в сумме с числом
, и число различных корней первого
уравнения в сумме с числом ![]() дает число различных
корней второго уравнения. Решить первое уравнение при каждом значении параметра,
выбранном таким образом.
дает число различных
корней второго уравнения. Решить первое уравнение при каждом значении параметра,
выбранном таким образом.
Часть I
(Записать краткое решение и номер полученного ответа)
А1. Дополнить утверждение: «Для того, чтобы плоскости совпадали, …, чтобы они имели две общие точки»
1) необходимо 2) достаточно
3) необходимо и достаточно 4) нет нужного варианта ответа
А2. Дополнить утверждение: «Для того, чтобы прямая лежала в плоскости, …, чтобы она имела с плоскостью одну общую точку»
1) необходимо 2) достаточно
3) необходимо и достаточно 4) нет нужного варианта ответа
А3. В следующее высказывание: «Боковое ребро наклонного параллелепипеда может быть перпендикулярно … основания» вставьте нужную по смыслу фразу:
1) одной стороне 2) двум сторонам
3) трем сторонам 4) плоскости
А4. В следующее высказывание: «Если две плоскости перпендикулярны, то …. перпендикулярна любой прямой, лежащей в другой плоскости» вставьте нужную по смыслу фразу:
1) любая прямая, лежащая в одной плоскости
2) прямая, перпендикулярная линии пересечения
3) прямая, параллельная линии пересечения
4) нет нужного варианта ответа
А5. Отрезок длиной 10 см пересекает плоскость, концы его удалены от плоскости на 2 см и 4 см. Найти проекцию отрезка на плоскость.
1) 5 см 2) 6 см 3) 4 см 4) 8 см
А6.
Длина образующей конуса равна 17, а
длина окружности основания ![]() , найти объем конуса.
, найти объем конуса.
1)
![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]()
А7. Расстояния от точки А до вершин квадрата равны 5. Найти расстояние от точки А до плоскости квадрата, если сторона квадрата равна 6.
1)
5 2) 3 3) ![]() 4) 4
4) 4
А8. Найти площадь поверхности правильного тетраэдра, если длина его ребра равна 3.
1) ![]() 2)
2)
![]() 3)
3) ![]() 4) 18
4) 18
А9. Прямые АВ, АС и АD попарно перпендикулярны. Найти длину отрезка СD, если АВ = 1 см, ВС = 13 см, АD= 11 см.
1)
17 см 2) 18 см 3) ![]() см 4)
см 4) ![]() см
см
А10. Найти радиус шара, если площадь его поверхности численно равна объему шара.
1) 1 2) 2 3) 3 4) 4
(Записать полное решение и полученный ответ)
В1. В прямой треугольной призме стороны основания равны 6, 8, 10, а высота равна 8. Найти площадь ее полной поверхности.
В2. Диагональ куба равна 9. Найти площадь полной поверхности куба.
В3.
Плоский угол при вершине правильной
треугольной пирамиды равен ![]() . Площадь боковой
поверхности пирамиды равна 192. Найти радиус окружности, описанной около боковой
грани пирамиды.
. Площадь боковой
поверхности пирамиды равна 192. Найти радиус окружности, описанной около боковой
грани пирамиды.
В4. В основании прямоугольного параллелепипеда лежит квадрат площадью 16см2. Через одну из сторон нижнего основания и противоположную сторону верхнего основания проведена плоскость. Площадь полученного сечения равна 20 см2. Чему равна полная поверхность параллелепипеда?
В5. Высота правильной треугольной пирамиды равна 6 см. На расстоянии 3 см от вершины проведена плоскость, параллельная основанию. Площадь полученного сечения равна 5 см2. Найти объем данной пирамиды.
В6. Образующая конуса равна 5 см, а диаметр его основания равен 6 см. Найти площадь поверхности шара, вписанного в конус.
В7. Развертка боковой поверхности цилиндра – квадрат, площадь которого равна 16/25. Найти объем цилиндра.
В8. В правильной четырехугольной пирамиде двугранный угол
при боковом ребре равен ![]() . Найти синус угла между
боковым ребром и плоскостью основания.
. Найти синус угла между
боковым ребром и плоскостью основания.
В9. Ребро правильного тетраэдра равно 2. Найти отрезок, соединяющий середины скрещивающихся ребер.
В10. Основание прямой призмы – ромб, а площади диагональных сечений равны 9 и 40. Найти площадь боковой поверхности призмы.
В11.
Одно из двух взаимно перпендикулярных
сечений шара проходит через его центр. Площадь меньшего сечения равна ![]() , а расстояние от центра шара до второго сечения равно
2. Найти площадь второго сечения.
, а расстояние от центра шара до второго сечения равно
2. Найти площадь второго сечения.
В12.
Диагонали граней куба служат ребрами
правильного тетраэдра. Площадь поверхности тетраэдра равна ![]() . Найти ребро куба.
. Найти ребро куба.
В13.
Основание прямоугольного
параллелепипеда ![]() – квадрат со стороной 4. Угол
между прямыми CB1 и C1D равен
– квадрат со стороной 4. Угол
между прямыми CB1 и C1D равен ![]() . Найти высоту
параллелепипеда.
. Найти высоту
параллелепипеда.
В14. В правильной треугольной пирамиде боковое ребро в 4,5 раза больше
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.