![]() .
.
При реализации расчетного алгоритма относительно уравнений газовой динамики возникают трудности в определении значений функции в граничных точках, поскольку они выпадают из алгоритма расчета. Для определения этих функций вводится предположение , что на первом для раздаточного коллектора и последнем для сборного коллектора интервале по координате процесс описывается уравнениями одномерной газовой динамики канонического вида [1.1.10]:
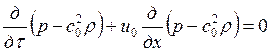
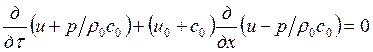 (13)
(13)
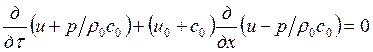
где ![]() и
и ![]() - скорость и плотность газа, и скорость звука в
невозмущенной среде.
- скорость и плотность газа, и скорость звука в
невозмущенной среде.
Система уравнений (13) хорошо описывает процессы при достаточно малых отклонениях давления, плотности и скорости газа от соответствующих значений в невозмущенной среде. Эта система решается методом характеристик. Из теории решения одномерных уравнений газовой динамики известно, что вдоль характеристик остаются постоянными некоторые величины, называемые инвариантами Римана, которые имеют вид :
![]() вдоль
вдоль ![]()
![]() вдоль
вдоль ![]()
![]() вдоль
вдоль ![]()
Для использования граничного условия, соответствующего выходу
из сборного коллектора, воспользуемся инвариантом Римана ![]() , с помощью которого можно связать параметры двух соседних
узлов с индексами k-1 и k на временных слоях m и m+1. Для входа в раздаточный коллектор примем
, с помощью которого можно связать параметры двух соседних
узлов с индексами k-1 и k на временных слоях m и m+1. Для входа в раздаточный коллектор примем ![]() , связывая параметры узлов с
индексами k=1 и k=2 на временных слоях m и m+1.
Эти отношения в сочетании с граничными условиями для входа и выхода, а также
уравнением энергии позволяют определить продольную скорость газа в начальной
(на входе в раздаточный коллектор) и в последней ( на выходе из сборного
коллектора ) точках неизвестного временного слоя при решении расщепленных
уравнений движения для скорости методом прогонки. Для определения плотности
, связывая параметры узлов с
индексами k=1 и k=2 на временных слоях m и m+1.
Эти отношения в сочетании с граничными условиями для входа и выхода, а также
уравнением энергии позволяют определить продольную скорость газа в начальной
(на входе в раздаточный коллектор) и в последней ( на выходе из сборного
коллектора ) точках неизвестного временного слоя при решении расщепленных
уравнений движения для скорости методом прогонки. Для определения плотности ![]() методом прогонки.
методом прогонки.
Для определения плотности ![]() на оси симметрии в силу наличия
особой точки r=0 уравнение неразрывности необходимо
преобразовать так, чтобы исключить из решения особую точку. Используя правило
Лопиталя и граничные условия, получим
на оси симметрии в силу наличия
особой точки r=0 уравнение неразрывности необходимо
преобразовать так, чтобы исключить из решения особую точку. Используя правило
Лопиталя и граничные условия, получим 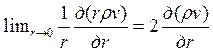 .
.
Тогда уравнение неразрывности для оси симметрии примет вид
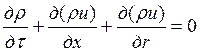 (15)
(15)
Уравнение (15) решается по “второй” схеме с разностями против потока.
В качестве граничного условия, соответствующего входу в
раздаточный коллектор, задается полное давление ![]() .
Для расчета статического
давления используем выражение
.
Для расчета статического
давления используем выражение
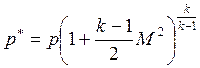 , где k-
показатель адиабаты;
, где k-
показатель адиабаты; ![]() ,
, ![]() -скорость звука.
-скорость звука.
Одним из основных условий устойчивости решения
нестационарных уравнений газовой динамики является правильный выбор шага
интегрирования по времени. Обычно для устойчивого решения уравнений движения
несжимаемой жидкости полагают число Куранта ![]() [1.1.9]
[1.1.9]
В потоке сжимаемой жидкости скорость распространения возмущения меняется в зависимости от градиента давления. Учитывая, что малое возмущение давления газа распространяется с местной скоростью звука a во
Всех направлениях, скорость распространения возмущения в
сжимаемой среде равна ![]() , а соотношение для числа Куранта имеет
вид [1.1.9]
, а соотношение для числа Куранта имеет
вид [1.1.9]
![]() (17)
(17)
В работе [1.1.9] отмечается, что
такая запись числа Куранта справедлива и для больших возмущений давлений,
причем скорость звука заменяется скоростью ударной волны. Таким образом,
ограничение шага по времени ![]() , в основном определяется значением
скорости звука. При расчете двумерных задач число куранта определяется по
соотношению [1.1.9]
, в основном определяется значением
скорости звука. При расчете двумерных задач число куранта определяется по
соотношению [1.1.9]
![]() .
(18)
.
(18)
Результаты расчета и их сопоставление с опытными данными
Предложенный метод решения системы дифференциальных уравнений в частных производных, описывающих течение газового теплоносителя в тепловыделяющей сборке с шаровыми твелами и с радиальным течением, была использована для расчета полей скорости и давления при изотермических условиях течения в раздаточном и сборном коллекторах и в пористом слое шаровых твелов, заполненным шарами с диаметром 26 мм.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.