Интенсификация и моделирование теплообмена в энергодвигательных установках аппаратов для пилотируемой экспедиции на Марс, страница 3

Последние члены уравнений движения (1) и (2) и третий член в правой части уравнения энергии  (5) отличны от нуля только пр моделировании процессов ,

Происходящих в шаровой засыпке. Система уравнений  (1)-(5) записана без учета диссипации механической энергии  в предположении, что газ – идеальный . Система уравнений (1)-(5) решается численными методами по достаточно малым участкам , поэтому можно принять, что коэффициенты вязкости  являются постоянными в окрестности каждого расчетного узла и вынести  их за знак дифференциала. Коэффициент гидравлического сопротивления засыпки по каждому из направлений при Re<2000 определялся по формуле [1.1.7]:

 , где для слоя из гладких шаров К=4.55- константа Козени  и =0.45 – для составляющей коэффициента . Эквивалентный критерий Рейнольдса

 определяется по  истинной средней скорости потока в пространстве между шаровыми элементами  и эквивалентному гидравлическому диаметру [1.1.7]. Для слоя шаров одинакового диаметра  (d-диаметр шарового твэла). Для области больших значений

 коэффициент  равен [1.1.7]

. Расчет коэффициентов турбулентной вязкости и теплопроводности двумерного потока с возвратными токами и переменной массой представляется особенно трудным из- за недостатка и противоречивости опубликованных данных. Величины коэффициентов турбулентной вязкости , полученные в [1.1.6] для полностью развитого турбулентного потока для круглой трубы  с пористыми стенками  и равномерным вдувом и для трубы без вдува, почти не различаются. Наиболее значительны расхождения  лишь для пристеночной области при значениях

y/R<0.2, где   R- радиус трубы, y- расстояние от стенки трубы. Поэтому  для определения пути перемешивания  внутри сборного коллектора используется эмпирическая формула Никурадзе:

                  (9)

Для раздаточного коллектора можно принять , что в пограничном слое , прилегающем к стенке, путь перемешивания равен , а во внешней части пограничного слоя составляет 1/10 толщины этого слоя, и при слабой интенсивности отсоса величина коэффициента турбулентной вязкости может быть принята такой же , как для трубы.

Коэффициент эффективной вязкости шарового слоя принимается как для стационарного зернистого слоя в виде функции, зависящей от скорости фильтрации w и характерного для потока линейного размера [1.1.7],  , где D- коэффициент . Для расчета коэффициента эффективной теплопроводности слоя твелов использовалась зависимость, учитывающая теплопроводность шаровых элементов и теплоносителя, конвекцию и тепловое излучение в различных газовых средах с точностью  [1.1.8]:

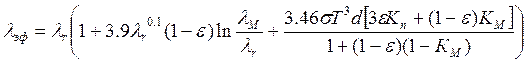,  (10)

где  -постоянная Стефана-Больцмана, и   соответственно степень черноты  поры и материала шаровых элементов. В методике предусмотрен расчет эффективного  коэффициента теплопроводности для пористой среды с учетом эффектов перемешивания [1.1.7]. В этом случае уравнение (10) должно содержать дополнительный член, учитывающий мольный и турбулентный перенос, вида

,                                                                                          (11)

где  -коэффициент, зависящий от упаковки шаров , u- скорость фильтрации, d-диаметр шара. Коэффициент турбулентной теплопроводности теплоносителя , протекающего в сборном и раздаточном коллекторах, определялся по формуле

,                                                                                                          (12)

Полученной Кинни и Спэрроу в предположении , что турбулентные числа  Прандтля и Льюиса равны единице.

Задача решалась со следующими граничными условиями :

- на всех твердых границах AB, BC,CD, EF,FM, NO (рис.1) использовалось условие прилипания и непроницаемости, т.е. u=0 и v=0,  и для производных давления   или ;

- на входе в раздаточный коллектор DE задается температура Т=Твх, давление  и радиально составляющая скорости v=0;

-на выходе из сборного коллектора  ОР задано статическое давление  p=pвых, при v=0 и ;

-для оси симметрии АР величины , v=0, ;

-поток тепла через все твердые границы равен нулю,  или

;