Турбулентная вынужденная конвекция и потери давления в однофазном закрученном потоке, страница 15

Конечно, работа [133] несопоставима по качеству с достаточно сложными в реализации экспериментальными работами [115–131], выполненными на весьма высоком уровне. Таким образом, список работ [115–131], выполненных в шести лабораториях, ограничивает все известные автору систематизированные теплофизические исследования в условиях одностороннего корпускулярного нагрева. Рассмотрим основные результаты, полученные в этих работах.

Результатом работы [115] является массив опытных данных о КТН при кипении в закрученном потоке в условиях одностороннего нагрева, представленный в [117]. Массив включает в себя 75 точек, из них в [117] представлено 47 точек, полученных при давлении 1,0 – 3,7 МПа (в диапазоне 3,2 – 3,7 МПа 30 точек), массовой скорости 3000–16000 кг/(м²×с), температуре воды на входе 35–171 ^оС, коэффициенте закрутки k = 0,79, диапазон значений q_кр = (16,8–68,6) МВт/м². За значения КТН на внутренней стенке принимались максимальные значения из распределения плотности теплового потока по внутреннему периметру, полученного из численного решения краевой задачи теплопроводности. На основе анализа данных, авторы [115]  пришли к выводам, что критическая плотность теплового потока: значительно возрастает с ростом скорости потока воды (температура на входе и давление на выходе фиксированы); слабо уменьшается с ростом давления; уменьшается с ростом температуры воды на входе (скорость и давление воды на выходе фиксированы); слабо уменьшается с увеличением диаметра канала. Отмечая большой объем работы, проделанной в [115] следует заметить, что полученный массив экспериментальных данных о КТН вследствие разброса по режимным параметрам имеет разрозненный характер. Экспериментальные точки получены при разных сочетаниях давления, массовой скорости, недогрева, диаметра трубы, что, к сожалению, затрудняет их обобщение. Для расчета значений КТН в [117] предложено использовать модель Celata [89], в которой, для учета одностороннего нагрева, переходят к осредненной плотности теплового потока на внутреннем периметре с использованием пикового коэффициента F (F определяется как отношение плотности теплового потока в лобовой точке внутреннего периметра к плотности на внешнем периметре рабочего участка), закрутка потока учитывается увеличением скорости в  раз. Использование такой модифицированной модели позволяет согласовать расчетные и опытные данные в пределах 20%, но при этом в расчетное соотношение входят эмпирические константы.

В работе [119] приведены основные результаты исследований, проведенных в JAERI. Представленные в [119] опытные данные о теплообмене в режимах однофазной вынужденной конвекции и пузырьковом кипении в трубе без ленты и со вставленной лентой с коэффициентом закрутки k = 0,52 были получены обработкой измеренных распределений температуры в стенке трубы с использованием решения обратной задачи теплопроводности. Данные по однофазному теплообмену (см. рис. 1.14) представлены в виде сравнения опытных точек с расчетом по формуле (1.15) для незакрученного потока и по эмпирической формуле Гэмбилла [13] для закрученного потока:

Nu_з = Nu_пр×2.18/(p/2k)^0.08, где Nu_пр рассчитывается по формуле (1.15) и вводится поправка на неизотермичность в виде (m_ж/m_ст)^0.14.

Как видно из рис. 1.14, опытные данные представлены с большим разбросом. Введение поправки на закрутку в виде 2.18/(p/2k)^0.08 приводит при                   k = 0,52 к увеличению числа Nu в два раза, тогда как эффект возрастания скорости закрученного потока, выражаемый комплексом , равен 1,13. По результатам сопоставления, представленным на рис. 1.14, авторы [119] делают вывод о возможности применения формул для расчета однофазного теплообмена для равномерно нагреваемых труб и в условиях одностороннего нагрева.

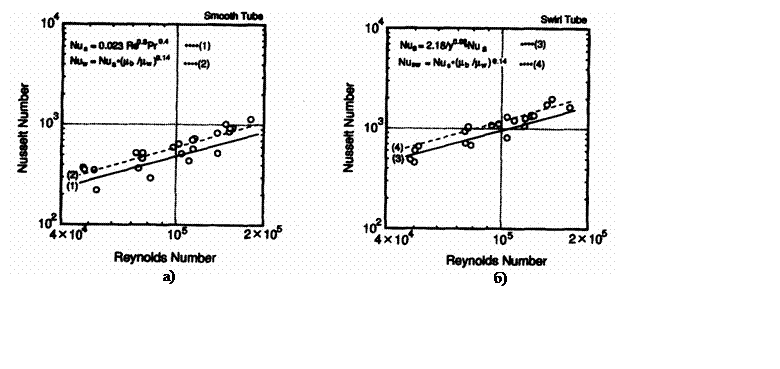
Рис.1.14. Данные по однофазному теплообмену [119], а) – незакрученный поток, б) – закрученный 

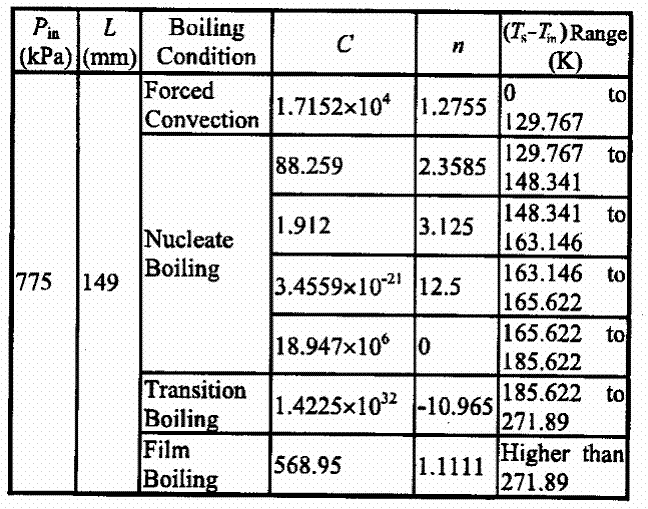
Данные о теплообмене при кипении в закрученном потоке представлены в [119] в виде расчетных зависимостей q(DT_s) для одного из режимов течения. Данные о значениях КТН в [119] не представлены. Для расчета теплообмена при кипении предложена зависимость, аналогичная формуле (1.21), с несколько измененными коэффициентами.