Турбулентная вынужденная конвекция и потери давления в однофазном закрученном потоке, страница 14

·  Sieder – Tate 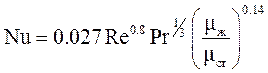                       .                                                     (1.16)

·  Петухов 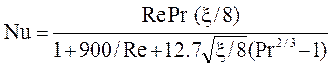                   .                           (1.17)

Расчет числа Re осуществлялся по гидравлическому диаметру, закрутка потока учитывалась увеличением скорости в  раз. Причем при проведении расчетов коэффициент теплоотдачи увеличивался в 1.15 раз, как поясняется, так учитывался эффект оребрения канала лентой.

Для режима поверхностного кипения

Плотность теплового потока при поверхностном кипении в вынужденном недогретом потоке воды рассчитывалась как:

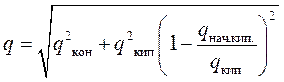,                                  (1.20)

где плотность теплового потока начала кипения q_{нач.кип} определялась по методике [132].

Процедура согласования расчётных и экспериментальных полей температуры в рабочем участке дала следующие результаты [115]:

·  вычисления с  использованием соотношения (1.15) в конвективном режиме показали плохое согласие с температурными измерениями. Результаты, полученные с использованием соотношений  (1.16) или (1.17) оказались значительно в бóльшей степени соответствующими экспериментальным данным.

·  в режиме поверхностного кипения расчеты при использовании соотношений (1.18) и (1.19) дают плохое согласие с температурными измерениями. Приемлемое согласие достигается при коррекции (1.18) в виде:

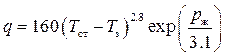.                                      (1.21)

Соотношения (1.15) – (1.20), а также несколько подобных эмпирических формул использовались при сопоставлении результатов температурных измерений с расчетом по прямой задаче теплопроводности и в работе JAERI [119]. По результатам сопоставления авторы [119] делают вывод о соответствии измерений и расчетов в пределах ± 30% и о необходимости построения новых уравнений, более точно описывающих теплообмен в условиях одностороннего нагрева.

Очевидно, что полученное авторами [115] и [119] расхождение расчетов с измерениями при одновременном использовании (1.18) и (1.20) связано с тем, что эмпирическое уравнение (1.18) описывает полную плотность теплового потока от стенки, а не вклад составляющей за счет кипения. Использование процедуры численного решения краевой задачи теплопроводности для получения опытных данных о теплообмене в условиях одностороннего нагрева требует тщательно выполненной верификации полученных результатов, сопоставления их с данными, полученными альтернативным путем. К сожалению, такого сопоставления для данных [115–132] в этих работах нет. Использование для верификации расчета сопоставления расчетных и опытных данных о температурах в некоторых точках рабочего участка не всегда достаточно, и может даже приводить к курьезным зависимостям для теплообмена, полученным, например, в работе [133]. В этой работе представлено численное исследование теплообмена и КТН в охлаждающих трубах дивертора термоядерной установки LHD (Япония). Имея в своем распоряжении экспериментально определенную зависимость q(T_ст–Т_ж.вх)  для докризисного теплообмена в круглой односторонне нагреваемой медной трубе с внутренним диаметром  9 мм, при р_вх=0,78 МПа и скорости потока воды 9,9 м/с, авторы [133] добавили собственные расчетные зависимости для переходного и пленочного кипения. Используя для задания теплообмена на внутреннем периметре трубы уравнение  q= С(T_ст–Т_ж.вх)ⁿ и применяя код CFD, авторы [133] подобрали значения постоянной С и показателя степени n, при которых наблюдается наилучшее соответствие между определенной в опыте и полученной расчетом зависимости q(T_ст–Т_ж.вх). Подобобранные значения С и nработы [133], опровергающие все известные закономерности одно- и двухфазного теплообмена, приведены в таблице 1.2. Авторы [133] использовали полученные результаты для определения временных характеристик прогрева и значений КТН для реальных диверторных приемников.

Таблица 1.2. Значения постоянной С и показателя степени n в зависимости для теплообмена q= С(T_ст–Т_ж.вх)ⁿ работы [133].