Турбулентная вынужденная конвекция и потери давления в однофазном закрученном потоке, страница 13

Мощные установки НИИЭФА им. Ефремова и JAERI использовались в основном для экспериментальной проверки работоспособности сборок диверторных и пучковых приемников. Работы [121–123] посвящены численному моделированию теплогидравлических процессов в диверторных приемниках.

Основная методическая сложность в интерпретации результатов первичных температурных измерений в исследованиях [115–131] связана с определением температуры стенки и плотности теплового потока на внутренней стенке канала. Для этого, в каждом из шести перечисленных коллективов, были независимо разработаны методики численного решения двухмерной краевой задачи теплопроводности в мишени рабочего участка. В исследованиях [115], [119], [123] и [130] решалась прямая задача теплопроводности. В этом случае задавались экспериментально измеренные плотность теплового потока на внешнем периметре и параметры потока воды, а варьировались расчетные формулы для коэффициентов теплоотдачи и соотношения, определяющие границы режимов. Критерием достоверности решения было соответствие расчетных и прямо измеренных температурных полей в рабочем участке. В исследованиях [119] помимо решения прямой задачи, было разработано и решение обратной задачи теплопроводности, которая решалась и в [125]. В этом случае по измеренному температурному полю в рабочем участке восстанавливались параметры теплообмена на внутреннем периметре. Достаточно подробно вопросы постановки и решения краевой задачи теплопроводности обсуждены в [119]. В любой постановке, в граничные условия на внутренней поверхности канала входит искомая температура этой поверхности. С неизбежностью возникает известная неопределенность, поскольку для рассматриваемых условий отсутствуют проверенные расчетные зависимости для теплообмена (особенно при пузырьковом кипении). Построение таких зависимостей является одной из основных целей исследований, а на этапе решения задачи теплопроводности используются обычные формулы, апробированные для равномерно нагреваемых труб.

В исследованиях [115] в граничные условия краевой задачи теплопроводности, решаемой на базе метода конечных элементов, на внутреннем периметре входили следующие соотношения для расчета теплоотдачи:

для режима конвективного теплообмена с учётом наличия скрученной ленты

·  Dittus – Boelter 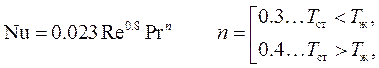      .                   (1.15)