Находим для исследуемого механизма угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.
Для начального звена во втором положении будем иметь:
![]()
![]()
Для остальных звеньев уравнения для центров масс и угловые ускорения находим по формулам:
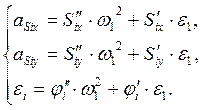 (4.1)
(4.1)
Результаты расчета по формулам (4.1) приведены в таблице 4.1.
Таблица 4.1
Ускорения центров масс и угловые ускорения звеньев
|
e1, 1/с2 |
aS2x, м/с |
aS2y, м/с |
e2, 1/с2 |
aS3x, м/с |
aS4x, м/с |
aS4y, м/с |
e4, 1/с2 |
e5, 1/с2 |
|
-6.2042 |
3.8357 |
-6.7985 |
9.0224 |
5.0511 |
-0.5147 |
-7.3526 |
18.5466 |
48.8947 |
- для звена 1
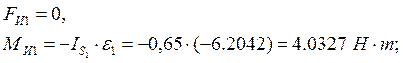
- для звена 2
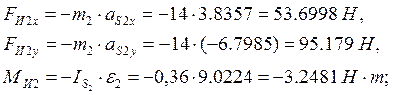
- для звена 3
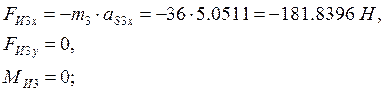
-для звена 4

-для звена 5
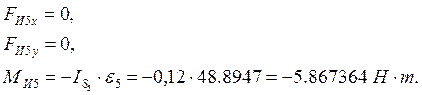
Для удобства работы сведем в табл. 4.2 все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.
Таблица 4.2
Силы и моменты действующие на механизм
|
Сила пресса, Н |
Силы веса, Н |
Силы инерции, Н |
Моменты сил инерции, Н×м |
|||||||
|
Fcx |
F2 |
F4 |
FИ2y |
FИ2x |
FИ3x |
FИ4y |
FИ4x |
MИ1 |
MИ2 |
MИ4 |
|
-11111 |
-137.2 |
-27.44 |
95.179 |
53.6998 |
-181.8396 |
20.5873 |
1.4412 |
4.0327 |
-3.2481 |
-0.92733 |
Так как направления сил и моментов учтены с их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а моменты – против хода часовой стрелки.
4.2.1 Исследование структурной группы 4 – 5 (рис. 4.1)
Для определения реакций в кинематических парах 01 и С, запишем два уравнения проекций сил на координатные оси и два уравнения моментов относительно точки D для звеньев 4 и 5:
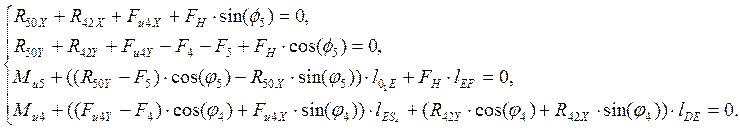 (4.2)
(4.2)
|
Рис. 4.1 |
Решая систему (4.2) MathCAD, найдем:
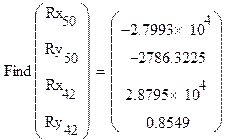
Реакции ![]() и
и ![]() определяем соответственно:
определяем соответственно:
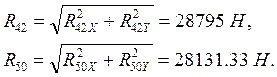
Реакцию ![]() , действующую в кинематической паре D,
находим из уравнения равновесия, например,
, действующую в кинематической паре D,
находим из уравнения равновесия, например,
звена 5:
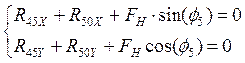
откуда
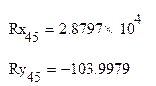
Полная реакция будет:
![]()
4.2.2 Исследование структурной группы 2 – 3 (рис. 4.2)
|
Рис. 4.2 |
Для определения реакций в кинематических парах 02 и А, запишем два уравнения проекций сил на координатные оси и два уравнения моментов относительно точки В для звеньев 2 и 3:
Проекции ![]() и
и ![]() найдены из анализа предыдущей группы:
найдены из анализа предыдущей группы:
![]()
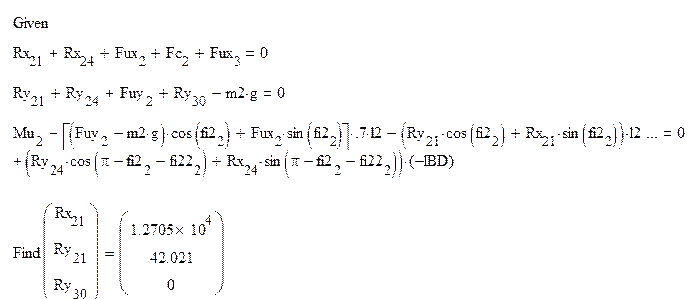 (4.3)
(4.3)
Реакцию ![]() определяем соответственно:
определяем соответственно:
![]()
Реакцию ![]() , действующую в кинематической паре B,
находим из уравнения равновесия, например, звена 3:
, действующую в кинематической паре B,
находим из уравнения равновесия, например, звена 3:
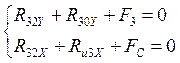
откуда
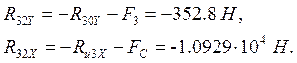
Полная реакция будет:
![]()
4.2.3 Определение уравновешивающего момента МУ и реакции R10 в кинематической паре А
|
Рис. 4.3 |
Для этого составим уравнения равновесия начального звена механизма (Рис. 4.3). Эти уравнения имеют вид:
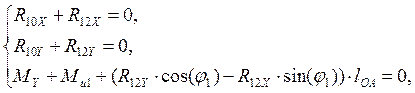
где ![]()
Решая систему получим:
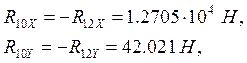
Реакцию ![]() определяем соответственно:
определяем соответственно:
![]()
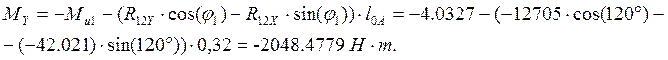
Теорема Жуковского: Если силу,приложенную к какой либо точке эвена плоского механизма, перенести параллельно самой себе в одноимённую точку повернутого на 90 градусов плана скоростей, то момент относительно полюса будет пропорционален ее мощности.
Если на звено действует момент пары сил, то его тоже необходимо перенести на план скоростей.
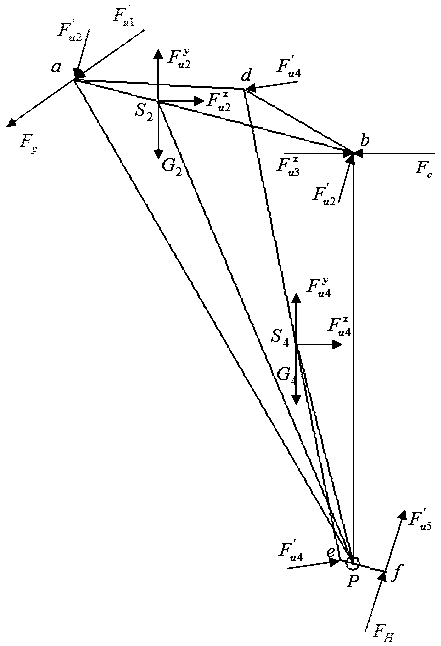
Рис. 4.4.
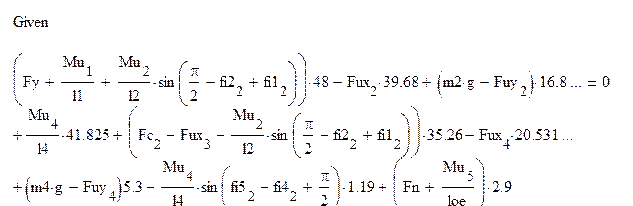
![]()
Далее определяем уравновешивающий момент Мy
My=Fy*0.32=-2048.49 Нм
Отклонение найденного с помощью рычага Жуковского значения момента Му от найденного аналитическим методом бедет:
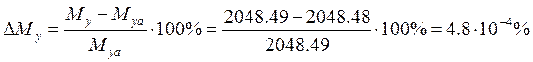
что значительно
меньше допускаемого для инженерных расчетов значения ![]() .
.
Все необходимые расчеты произведены в программе «MathCAD»и представлены в приложении.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.