БГУ
Химический факультет
Отчет по лабораторной работе № 1
«ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ ОБОРОТНОГО И МАТЕМАТИЧЕСКОГО МАЯТНИКОВ»
выполнили студенты
1 курса 1 группы
Шахно Дмитрий,
Бородич Ирина
Минск, 2010
Тема. Определение ускорения свободного падения при помощи оборотного и математического маятников.
Цель. Определить ускорение свободного падения с помощью оборотного и математического маятников с минимальной относительной погрешностью emin, не превышающей 5 %.
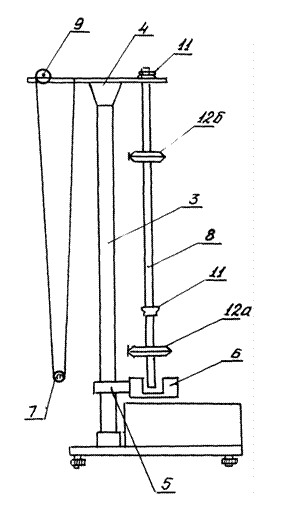
Рис. 1, где 1 – основание, 2 – регулируемые ножки , 3 – колонка, 4 – верхний кронштейн,
5 – нижний кронштейн, 6 – фотоэлектрический датчик, 7 – математический маятник, 8 – оборотный маятник, 9 – регулятор длины математического маятника, 11 – опорные призмы, 12(а, б) – чечевицы.
Расчетные формулы.
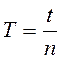 ,
(1)
,
(1)
где t – измеренное время, n – число колебаний, T – период колебаний.
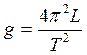 ,
(2)
,
(2)
где g – ускорение свободного падения, T – период колебаний, L(для математического маятника) – расстояние от конца оборотного маятника до опорной призмы , L(для оборотного маятника) - расстояние между опорными призмами.
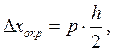 (3)
(3)
где ![]() - доверительная
вероятность,
- доверительная
вероятность, ![]() - цена деления измерительного прибора.
- цена деления измерительного прибора.
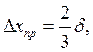 (4)
(4)
где ![]() - предельная максимальная
абсолютная погрешность.
- предельная максимальная
абсолютная погрешность.
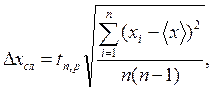 (5)
(5)
где ![]() - случайная погрешность,
- случайная погрешность,
![]() - коэффициент Стьюдента,
- коэффициент Стьюдента, ![]() - кол-во опытов,
- кол-во опытов, ![]() -
стандартное отношение.
-
стандартное отношение.
![]() (6)
(6)
![]() (7)
(7)
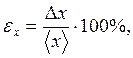 (8)
(8)
Выполнение работы.
Таблица 1. Результаты измерений периодов колебаний оборотного маятника.
|
d см |
n |
tпрям., с |
Tпрям., с |
tперев., С |
Tперев., С |
|
1 |
10 |
11,932 |
1,193 |
17,570 |
1,757 |
|
2 |
10 |
11,801 |
1,180 |
16,034 |
1,603 |
|
3 |
10 |
11,621 |
1,162 |
14,767 |
1,477 |
|
4 |
10 |
11,478 |
1,148 |
13,703 |
1,370 |
|
5 |
10 |
11,351 |
1,135 |
12,798 |
1,280 |
|
6 |
10 |
11,176 |
1,118 |
12,015 |
1,202 |
|
7 |
10 |
11,043 |
1,104 |
11,350 |
1,135 |
|
8 |
10 |
10,923 |
1,092 |
10,792 |
1,079 |
|
9 |
10 |
10,789 |
1,079 |
10,290 |
1,029 |
|
10 |
10 |
10,650 |
1,065 |
9,882 |
0,988 |
Таблица 2. Результаты измерений периодов колебаний оборотного маятника в прямом и перевернутом положениях при расстоянии (d) опорных призм от концов маятника, равном 8см.
|
N |
tпрям.,с |
Tпрям.,с |
tперев.,с |
Tперев,с |
|
10 |
10,941 |
1,094 |
10,901 |
1,090 |
|
10 |
10,929 |
1,093 |
10,895 |
1,090 |
|
10 |
10,924 |
1,092 |
10,908 |
1,091 |
|
10 |
10,931 |
1,093 |
10,913 |
1,091 |
|
10 |
10,935 |
1,094 |
10,891 |
1,089 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.