Силы межмолекулярного взаимодействия. Силы Ван-дер-Ваальса. Потенциальная кривая взаимодействия молекул

Лекция 15. СИЛЫ МЕЖМОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ. CИЛЫ ВАН-ДЕР-ВААЛЬСА. ПОТЕНЦИАЛЬНАЯ КРИВАЯ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ.

Модель идеального газа применима для реальных газов в том случае, когда расстояние между молекулами много больше размеров молекул.

Для небольших молекул воздуха (О₂, N₂, СО₂, Н₂О и т.д.), которым дышит человек при нормальном атмосферном давлении среднее расстояние между молекулами примерно в 30 раз больше среднего диаметра молекул .

С точки зрения классической физики: отрицательные электроны удерживаются в атоме за счет сил притяжения положительного ядра. В целом атом нейтрален.

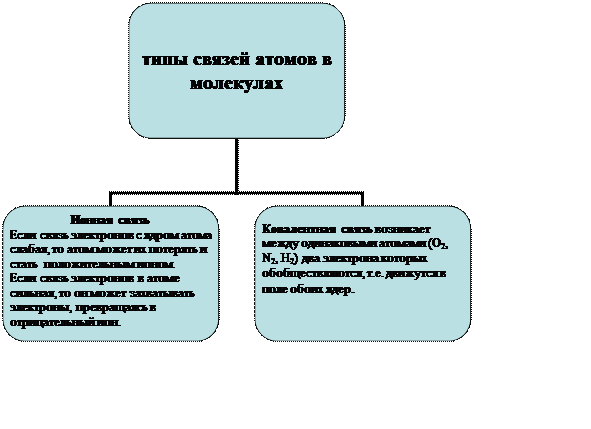
Ионная связь в молекуле обеспечивается электрическим взаимодействием положительного и отрицательного ионов, образующих молекулу.

Силами Ван-дер-Ваальса называются силы притяжения, действующие между молекулами на расстояниях сравнимых с размерами молекул.

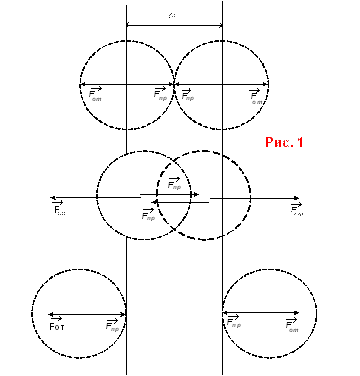
Эксперименты подтверждают, что силы взаимодействия между молекулами могут быть как силами отталкивания, так и силами притяжения (рис. 1).

 

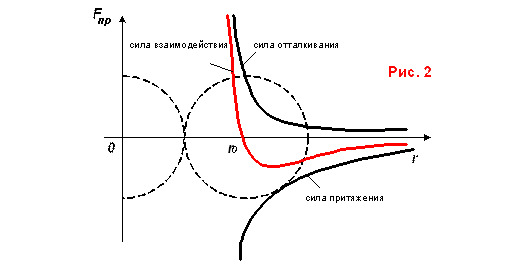Если связать начало системы отсчета с центром одной молекулы (рис. 2),зависимость потенциальной энергии взаимодействия от расстояния между центрами молекул имеет сложный характер, а величина потенциальной энергии взаимодействия молекул может быть рассчитана по формуле:     (1), где показатели степени зависят от конкретных свойств молекул.

Для многих молекул хорошее приближение дают n=12, m=6 и  зависимость потенциальной энергии:    (2).

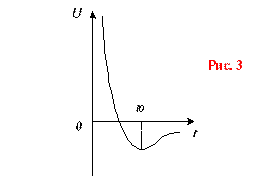
                                                                         (3)                                    

Из механики                                     (4)                                                            

При расстоянии (рис. 3) r=r₀   , а .

·  Силы межмолекулярного взаимодействия обеспечивают переход реальных газов, при определенных условиях, в жидкое состояние, т.е. процесс конденсации.

·  Для реальных газов уравнение Клапейрона-Менделеева не выполняется.

ГАЗ ВАН-ДЕР-ВААЛЬСА.  УРАВНЕНИЕ СОСТОЯНИЯ. КРИТИЧЕСКОЕ СОСТОЯНИЕ. ВНУТРЕННЯЯ ЭНЕРГИЯ ВАН-ДЕР-ВААЛЬСА.

I.Экспериментальное исследование реальных газов.

При изотермическом сжатии, например, аммиака при температуре Т₁ (опыт Ван-Марума) (рис. 4) зависимость давления от объема не подчиняется  закону  или .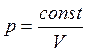

Насыщенным называется газ, находящийся в состоянии динамического равновесия со своей жидкостью.

Изотермами Ван-дер-Ваальса (рис. 5) называется набор экспериментальных зависимостей давления от объема для реальных газов.

В диапазоне  при  два фазовых состояния вещества: жидкость и насыщенный пар.

К – критическая точка;

V₂ – объем насыщенного пара;

- ненасыщенный пар;

V₁ – объем жидкости;

- только газ при любом давлении.

• При температуре Т_к изотерма Ван-дер-Ваальса имеет лишь точку перегиба с горизонтальной касательной.
• Жидкость и газ имеют одинаковые физические свойства, например, плотность жидкости равна плотности газа   , нет границы между жидкостью и газом (коэффициент поверхностного натяжения равен нулю)

Критическим называется такое состоянием вещества, при котором  физические свойства различных фазовых состояний одинаковы.

Критическими называются соответствующие этому состоянию параметры: критическая температура Т_к,  давление р_к, объем V_k.

Вещество в газовом состоянии при температуре выше критической T>T_k невозможно перевести в жидкое состояние ни при каком давлении.

 

II. Уравнение Ван-дер-Ваальса.

Уравнение Клапейрона – Менделеева  получено для идеального газа, т.е. в случае, когда силы  взаимодействия молекул не учитываются.

Как учесть силы отталкивания и притяжения между молекулами?

1)  Действие сил отталкивания приводит к тому, что в объем, занимаемый одной молекулой, не может проникнуть другая (рис. 6).

Объем недоступный для движения:   (5), где d – средний диаметр молекулы, V₀ – занимаемый ею объем.

Для одного моля идеального газа:

а) недоступный для движения молекул объем   b=4V₀N_A    (6),

б) объем, в котором молекулы могут двигаться    (7),  где - объем, занимаемый молем реального газа.

2)  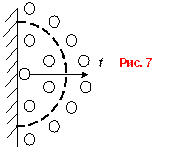Так как в реальном газе существуют силы притяжения между молекулами, то  молекулы возле стенки притягиваются внутренними молекулами. Поэтому возникает дополнительное эффективное давление , пропорциональное числу молекул, приходящейся на единицу площади, а также результирующей силе притяжения другими молекулами (рис. 7)(также на единицу площади)     .

  (8)  . Концентрация молекул для одного моля газа 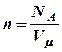     (9).

Поэтому дополнительное давление 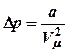  (10), где а =const, зависящая от природы молекул и количества газа.

Уравнением Ван-дер-Ваальса называется уравнение состояния реального газа:

для одного моля газа: 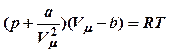   (11),

для  молей газа: 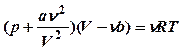  (12).

Соответствует ли это уравнение реальным изотермам Ван-дер-Ваальса?

Преобразуем уравнение для одного моля:   (13).

Полученное уравнение третьей степени, т.е. имеет три значения объема моля для каждого значения давления, и соответственно дает набор теоретических изотерм Ван-дер-Ваальса.

 

                                                     

                                                                                           

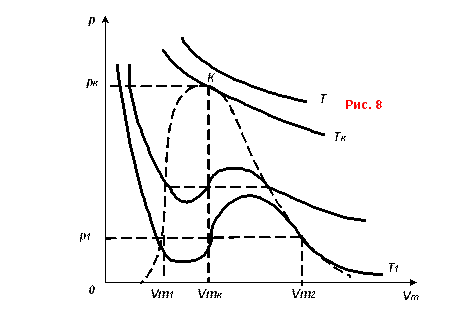
теория и эксперимент (рис. 8 и рис. 9)

Сравнение с экспериментальными показывает:

·  на участках АB и EL теория и эксперимент согласуются;

·  на участке СD состояние вещества неустойчиво и не реализуется, т.к. уменьшению объема соответствует уменьшение давления;

·  участок СB  соответствует пересыщенному пару, т.е. по физическим свойствам это должна быть жидкость, но вещество остается в газообразном состоянии;

·  участок ED соответствует  перегретой жидкости, которая по своим параметрам должна быть газом, но остается в фазе жидкости.

Метастабильными называются состояния, которые не являются абсолютно устойчивыми, и при незначительном внешнем воздействии переходят в ближайшее устойчивое состояние.

Пересыщенный пар и перегретая жидкость являются метастабильными состояниями вещества.

Уравнение Ван-дер-Ваальса позволяет определить критические параметры.

При Т=Т_к        (14) и уравнение третьей степени можно записать:

    (15).

Из сравнения коэффициентов при одинаковых степенях молярного объема  

критические параметры:     (16),  (17),      (18).

Внутренняя энергия газа Ван-дер-Ваальса  определяется энергией хаотического движения молекул и потенциальной энергией взаимодействия молекул:

  (19), где  изохорная молярная теплоемкость.

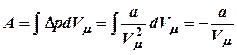,     (20).

Внутренняя энергия одного моля  газа Ван-дер-Ваальса 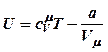      (21).