21. Продольные и поперечные волны. Уравнение плоской монохроматической волны.
Если в упругую среду поместить источник колебаний, то соседние с ним частицы среды также придут в колебательное движение. Эти частицы будут колебаться с одинаковыми периодами, но фазы колебаний частиц среды будут различны. Чем дальше расположена частица от источника колебаний, тем позже начнутся колебания. Распространение колебаний в среде называется волновым периодом, или волной. Направление, вдоль которого распространяется волна, называется лучом. Различают поперечные и продольные волны.
Поперечные – если частицы среды колеблются перпендикулярно лучу, т.е. такая волна является упругой волной сдвига.
Продольные – если частицы среды колеблются вдоль луча.
Продольная волна может возникать в среде, обладающей упругостью объема (ж, газ, тв). Поперечные волны возникают в среде, обладающей упругостью формы (тв).
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.
![]()
или, учитывая, что T= 1/n, где n — частота колебаний,
![]()
Получим уравнение плоской волны
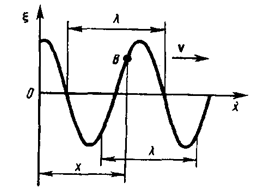
Пусть колебания источника О – гармонические и описываются
уравнением ![]() . Рассмотрим некоторую частицу С. Очевидно,
что если точка О колеблется t с,
то точка С будет колебаться меньше –
. Рассмотрим некоторую частицу С. Очевидно,
что если точка О колеблется t с,
то точка С будет колебаться меньше – ![]() . тогда уравнение колебания точки С, где
. тогда уравнение колебания точки С, где ![]() , равно:
, равно:
![]()
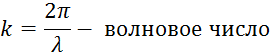
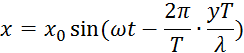
![]()
![]()
Знак ‘+’ указывает противоположное направление распространения волны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.