Волны. Уравнение волны, распространение волн в упругой среде. Энергия волны

Лекция 9. ВОЛНЫ. УРАВНЕНИЕ ВОЛНЫ. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ. ЭНЕРГИЯ ВОЛНЫ.

1)  Основные понятия и определения:

в широком смысле – процесс распространения в пространстве изменения связанных между собой физических величин

Волна:                                            .

                    

в узком смысле –     процесс распространения в пространстве периодически изменяющейся  физической величины

                                                      .

а) полевой характер физических величин, т.е. физические  

величины определены в каждой точке области распространения

                                              волны и изменяются непрерывно;

                                              

Условия                  

существования              б) изменение физической величины в одной точке должны вызывать

волны:                                 с некоторым запаздыванием изменения этой же величины в ближайшей окрестности этой точки.

2) 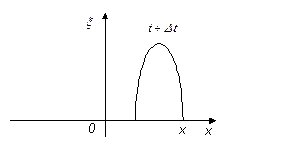 Уравнение волны (простейший случай – волна распространяется вдоль одной прямой 0х) 

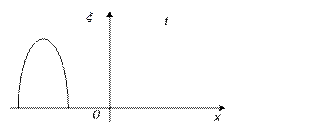
Пусть  - какая либо физическая величина (Е, р, х…), - скорость распространения волны.

Пусть в точке х=0 физическая величина изменяется по гармоническому закону

 (1), где - циклическая частота колебаний источника волны.

В точку с координатой х  возмущение  придет с запаздыванием на           :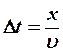

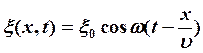   (2) - уравнение гармонической бегущей волны

                                                                характеристики волны

амплитуда волны         фаза волны             период волны         фазовой скоростью

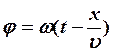
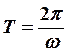                                                            скоростью распространения

                                                                                                               определенная фаза колебания

длина  волны                                                   волновое число

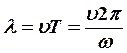
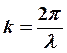                                                        (3)                        Фронт волны

                                                                                                                    (волновая поверхность)  геомет. место точек, колеб. в одинаковой фазе

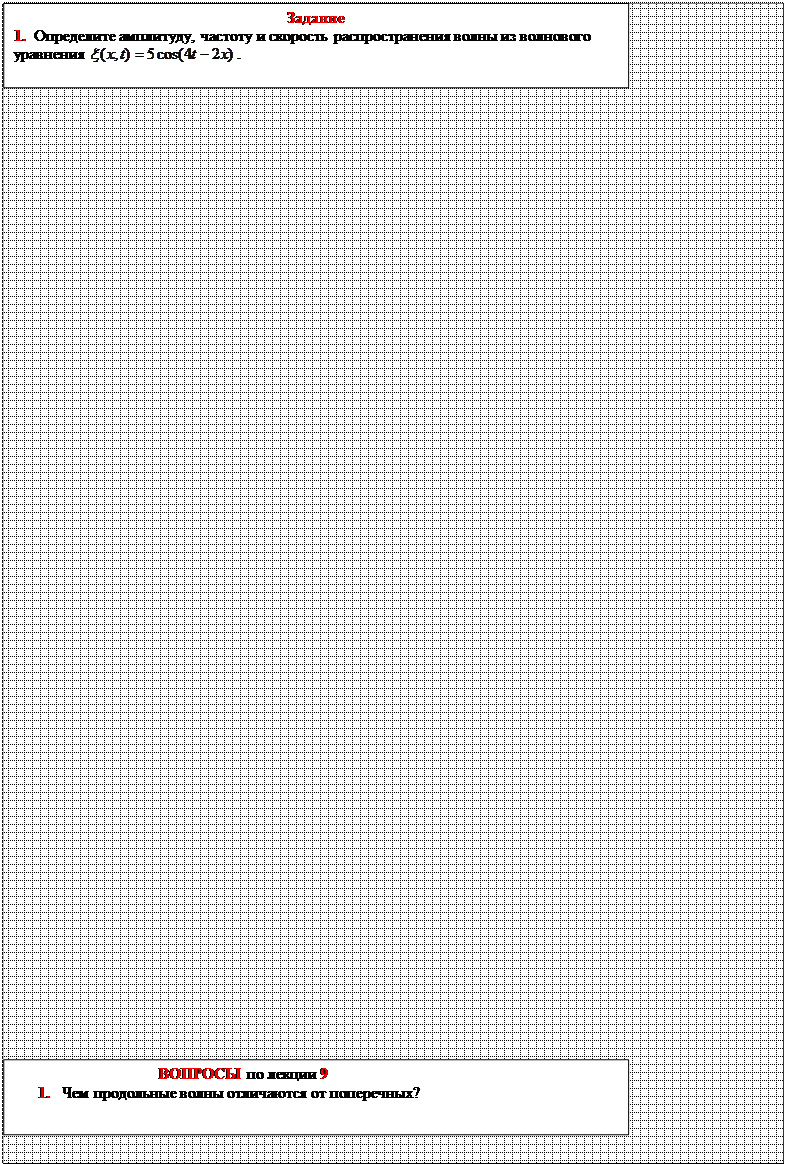Преобразуем: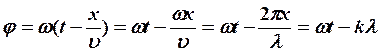  

(2)                 (4)    

 

Словосочетание «колебания частиц совпадают по фазе» используют для тех частиц, участвующих в волновом процессе, которые в данный момент имеют одинаковые смещения от положения равновесия и одинаковые проекции  скорости. На самом деле фазы этих частиц отличаются на  ,  где n –четное число.

Длиной  волны называется расстояние, на которое распространяется волна за период или минимальное расстояние между точками среды,  колеблющимися в одинаковой фазе.

                                                                                                     

Источником волны называется колеблющееся тело, возбуждающее волновое движение.

  В случае волны, распространяющейся вдоль оси 0x для таких точек 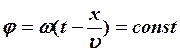 и при =const, в фиксированный момент времени t  x=const, т.е. фронт волны – плоскость, перпендикулярная оси 0x.

                                                                        фронт волны

плоский  (волна плоская)                                           сферический   (волна сферическая)

                                          

3) Волновое уравнение.

Найдем частные вторые производные  и  из уравнения волны (4):

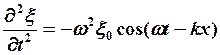
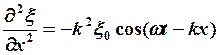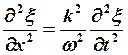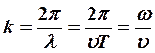  или  , т.к. учитывая (3) , то

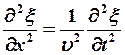   (5) - волновое уравнение описывает любой волновой процесс, протекающий с постоянной скоростью.

 

4) Волны в упругой среде.

а)   деформация сжатия – растяжения, возникшая  

в каком либо сечении упругой среды, после прекращения внешнего воздействия распространяется в среде вдоль направления   

деформации.

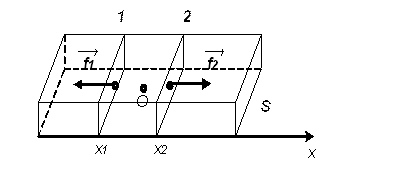
Физическая величина   - смещение центра масс малого объема точки О,  и  упругие силы, действующие на грани этого объема

По второму закону Ньютона 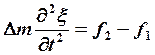    (6), где 

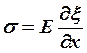    , по закону Гука , где

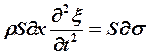  (7) 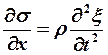                         , т.к.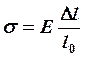                      

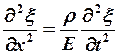      (8) - волновое уравнение при распространении продольной волны.

сравним (5) и (8) 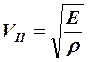                                 (9) – скорость упругой продольной волны ( )

б)   деформация сдвига распространяется в среде в направлении перпендикулярном направлению  деформации

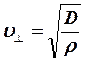Волна поперечная ( )                         (10) D – модуль сдвига

5) Энергия волны

Механическая  волна не переносит вещество, а переносит энергию колебательного движения.

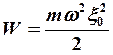, где m – масса единичного объема вещества,

- циклическая частота колебаний источника волны,

- амплитуда колебаний частиц среды.

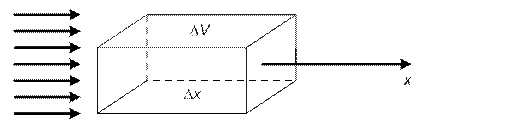
Пусть плоская волна распространяется со скоростью   и в малый объем  через поверхность S за

промежуток времени  поступила энергия  , где 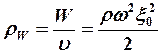   - энергия единичного объема,  - плотность вещества.

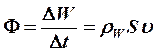     (11)- поток энергии,  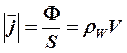- плотность потока энергии, 

    (12) - вектор Умова.