Intraparticulate difusion. Extension of the concepts of thiele modulus and efficiency

INTRAPARTICULATE DIFUSION

The porous structure of the catalyst grains implies a problem of access. In fact, the development of a structure designed to increase the surface area per unit volume of reactor would be inadequate if, simultaneously, difficulties of access to this surface compromised the gain realized in catalyst volume. This is why the paths of the reactants and products in the porous medium making up the catalyst mass must be examined closely.

We shall examine this problem in the ideal case of an isothermal catalytic reaction occurring in a spherical porous grain of homogeneous structure, i.e. with active sites uniformly distributed in the granular volume. Figure 10.2 shows a spherical layer inside the grain, and we shall now make a mass balance around this layer.

Consider a catalyst grain with radius R, immersed in a fluid containing a reactant A, which, in contact with the catalyst, gives rise to the reaction whose stoichiometric equation is written:

n₁A₁+n₂A₂=0

We shall consider a rate expression of the form r'=k_MC₁, i.e.. a first-order reaction, where r' is expressed in mol/s . kg of catalyst. (In these conditions, the rate constant k_M is expressed in m³/s . kg.) Introducing an effective diffusion coefficient   , we can use an expression similar to Fick's law to make a molar balance around the spherical layer of thickness dz. We shall write that, whatever enters the layer at radius z, plus what appears in the layer, is equal to what leaves the layer at radius z + dz, in steady-state conditions.

Fig. 10.2. Diffusion fluxes in spherical layer cut in a spherical catalyst grain and typical concentration profile in the grain.

For reactant A₁, the material entering at radius z per unit time is:

The following appears in the layer:

(since n₁ is negative, this actually represents a disappearance) and the following leaves at radius z + dz

After development and simplification, the balance is written:

with  (10.6)

This differential equation must be solved with the following boundary conditions:

C_1R is the concentration of A₁ existing at the external surface of the grain,

 (for the sake of symmetry)

Changing the variable            , we can write:

(10.7)

with                                                                                                                         (10.8)

The general solution to (10.7) is written:

The boundary conditions are then expressed by:

We therefore have:

and

Ф, defined by (10.8), is a dimensionless number called the Thiele modulus. It can also be expressed by:

(10.9)

As we shall show, it plays the same role as the Hatta number for gas/liquid reactions.

The solution of (10.6) is finally written:

(10.10)

If we develop sh [z/R] in series in the neighborhood of z = 0, we obtain:

and consequently

By deriving expression (10.10), we obtain:

This expression is always positive.

A typical concentration profile is shown in Fig. 10.2. The net number of moles of A₁ penetrating by diffusion into the particle to react therein is expressed by:

(10.11)[1]

Since (dC_1z/dz) is positive, a negative value is obtained for    , and this is normal: this is an entering flux in the direction of decreasing z values:

(10.12)

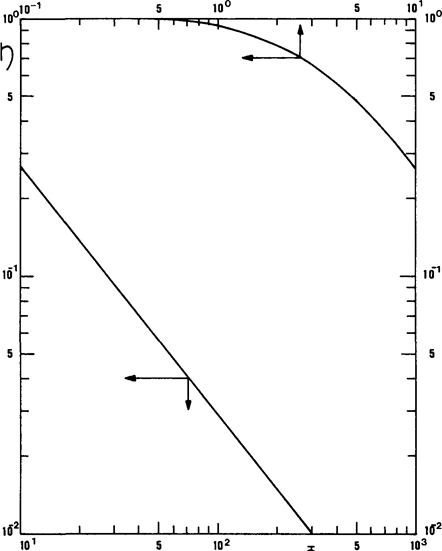
Fig. 10.3. Relationship between efficiency and Thiele modulus.

 Isothermal, isochoric first-order reaction in spherical grains.

If the diffusion of reactant A₁ was sufficiently rapid for concentration C_1R to exist at every point of the particle, the entering flux would be equal to the reaction rate with respect to the grain:

-N_1R (without diffusion limitation) =                                                                (10.13)

As in the case of fluid/fluid reactions, we can therefore define an efficiency h

(10.14)

Figure 10.3 shows the variations of h as a function of Ф for spherical particles and an irreversible first-order reaction, taking place isothermally in the grain. With the introduction of efficiencyh, the flux of A₁, and hence the rate of transformation ofA₁, per grain, is written:

(10.15)

It appears that happroaches 1 with decreasing Ф; in other words, if the particles are small, the reaction is slow, or diffusion is easy.

The obvious practical conclusion is that active catalysts (high k_M) should always be used in the smallest possible size, in accordance with the other requirements to be met (especially pressure drop across the bed). Another interesting practical conclusion is that it may be advantageous to deposit the active catalyst substances only in the external layer of the porous grains, with no intention of employing the entire pore volume available.

10.3. EXTENSION OF THE CONCEPTS OF THIELE