Intraparticulate difusion. Extension of the concepts of thiele modulus and efficiency, страница 5

L is the thickness of the catalytic porous plate, the other dimensions of the plate being very large in comparison with this thickness, and transfer being assumed to occur by only one side of the plate.

It should be recalled that in the Thiele modulus:

n₁           = stoichiometric coefficient of transferred reactant A₁,

L    = characteristic length equal to the thickness of the porous plate (m),

= effective diffusion coefficient of component A₁ (m²/s),

= product of a rate constant k_M (m³/kg . s) multiplied by a porous plate density     (kg/m³), making an entity whose dimension is s^-1.

Moreover, it is still possible to define:

(10-5)

taking the definition of

This also leads to e_p =          , where e_p is the fraction of volume of reactor occupied by the grains.

Furthermore, with respect to the Hatta number, we have written for       a first-order reaction:

(see Chapter 7)

In this expression:

n₁= stoichiometric coefficient of transferred reactant A₁.

= characteristic length equal to the film thickness in phase II (m),

= diffusion coefficient of A₁ in phase II (m²/s),

= rate constant (s^-1).

Hence a perfect correspondence can be observed in the respective dimensions of the Hatta number and the Thiele modulus, but with a significant difference:

(a) While the volume of the film of phase II, apart from extreme cases, accounts for only a small part of phase II, the volume of the porous film represents the entire porous reaction phase (compare L with     ).

(b) The term b=           for the case of the fluid/fluid reaction consequently corresponds to the value 1 in the case of the fluid/solid catalyst reaction.

Hence, strictly speaking, it is only for the case b= 1 that the analogy is perfect, and that we can compare the efficiency terms, for example, for a first-order reaction with diffusion through a plane interface. In this case, in fact, we have:

                                         with                                           (7.43)           

and respectively

(10.25)

with

(10.26)

If we make b = 1, we obtain:

i.e. an identical expression for both mechanisms.

The comparison can be continued further, by comparing for example:

(7.44)

which can be written

with            being the observed rate of disappearance of reactant A₁           in mol/unit time. unit volume of reactor.

Whereas, in the other case, for a first-order reaction, we have:

 (10.27)

Introducing L =          we obtain:

 (10.28)

which has an absolutely identical form to Ha² .  if b = 1.

It is easy to show that the correspondence is maintained for other orders of reaction.

Note on the expression of the Thiele modulus and of 'efficiency'

in a plane system

Consider a porous catalytic plate exposed on one of its sides to reactant Ai reacting on the active sites according to v₁A₁® products. L is the thickness of the plate.

The basis is a unit interfacial area. A balance is made on the slice of thickness dz:

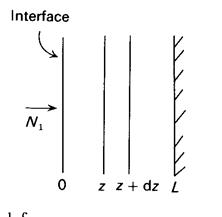with

from which

Consider a first-order reaction (n = 1) and let us define:

We have to solve:

with the boundary conditions

This leads to:

The net entering flux per unit interfacial area is equal to:

The flux that would enter in the absence of diffusion limitation would be equal to:

(without diffusion limitation) =

The efficiency h, the ratio of these two fluxes, is therefore:

10.5. INFLUENCE OF INTRAPARTICULATE DIFFUSION MECHANISMS ON THE SELECTIVITY OF CATALYTIC CHEMICAL REACTIONS

Since intraparticulate diffusion slows down a fast reaction more than a slow reaction, we can generally expect a decrease in selectivity if the faster reaction is desired. Wheeler [2] investigated the different alternatives. We shall relate the essential results.

10.5.1. Independent parallel first-order reactions