Intraparticulate difusion. Extension of the concepts of thiele modulus and efficiency, страница 2

MODULUS AND EFFICIENCY [ 3]

The concepts of the Thiele modulus and efficiency can be extended to the following cases:

(a) Non-spherical grains.

(b) Reactions with an order different from 1.

(c) Non-isochoric reactions.

(d) Non-isothermal reactions.

10.3.1. Geometric shapes other than the sphere

For particles consisting of long cylinders or long plates, calculations similar to those presented for spheres can be carried out. In actual fact, it appears preferable to employ the concept of equivalent diameter, and to use a Thiele modulus defined as:

(10.16)

10.3.2. Reactions with an order different from 1

In the same way as in defining a modified Hatta number for fluid-fluid reactions with an order different from 1 for the transferred reactant, a Thiele modulus is defined and generalized to n^th-order reactions with respect to reactant A₁:

(10.17)

In the case of more complex kinetic expressions, although the identical calculations are sometimes possible analytically, it is necessary, depending on the type of kinetic expression:

(a) Either to treat the kinetics concerned as an n^th -order reaction and to use Eq. (10.17).

(b) Or to integrate numerically the differential equation similar to Eq. (10.6) but containing the kinetic expression specific to the case concerned.

An elegant manner of dealing with the problem if the reaction order and rate constant are not simultaneously known, but if the reaction rate can be measured, consists in introducing the dimensionless Weisz number equal to  Ф²h, as shown below.

If we recall that the observable local rate of disappearance of reactant A₁ per unit volume of reactor (i.e. of catalyst bed) is equal to :

and that

we have

(10.18)

Ф²h can be calculated from the measured or estimated values of r_obs(A₁), d₁, C_1R, Д_1e,. and e_p.

Using the correlations                    for n = 0,1 and 2, it becomes possible to estimate hand hence to evaluate the degree of utilization of the catalyst for the reaction concerned (Fig. 10.4).

Figure 10.5 shows the concentration profile in terms of Ci/C^s according to the penetration depth z/R, for different orders of reaction, where

C_1s = concentration of components A₁ at the external surface of the particle,

C_1s ⁼ C_1R for a spherical particle.

10.3.3. Non-isochoric reactions

We have hitherto examined isochoric reactions such as:

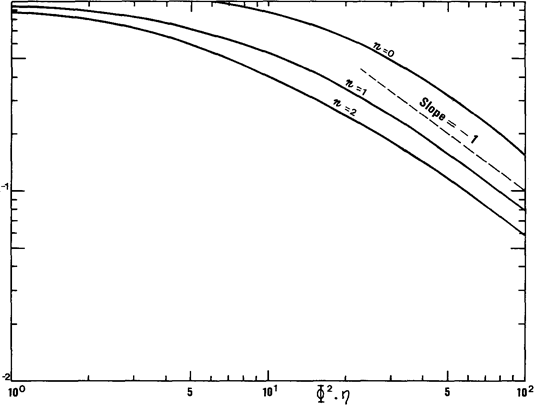
Fig. 10.4. Relationship between efficiency h and the function Ф²h

Isothermal, isochoric system, spherical geometry, order n.

Fig. 10.5. Concentration profiles in the grain, according to the value of Ф and order n.

In these conditions, for each molecule of A₁ transformed in the grain, one mole of product is formed, which will travel in the opposite direction to A₁ to leave the grain. This represents the case of equimolecular diffusion, to which the simplified form of Fick's law can be applied:

If v₂ is different from — v₁, the convection flux is superimposed on the diffusion flux and Fick's law is written:

with

= total concentration in mol/m³.

The writing of the mass balances then becomes complex, and it is impossible to find an analytical solution for C_1z= f{z). As a rule:

(a) If v₂ > (—v₁) the efficiency decreases.

(b) If v₂< (—v₁), the efficiency increases.

Weekman and Gorring [4] introduced the volume change modulus :

(10.19)

where

C_1s = concentration of reactant A₁ at the external surface of the grain,

SCis = sum of the concentrations of all the compounds (including inerts) at the external surface of the grain,

and succeeded in calculating the ratio of efficiency h_v (with change in volume) to that without change in volume h for different values of reaction order, Thiele modulus Ф and modulus w. Analyzing their conclusions, we can observe that h_v /h remains between 0.7 and 1.3 for the usual values of: