Эрроу и Гурвиц ставили задачу следующим образом.
Группа людей приходит на рынок торговать, каждый торговец приходит со своим товаром. Торговцы договариваются о следующей процедуре, Они выбирают начальную цену каждого типа товаров. Затем каждый вычисляет в этих ценах стоимость своего запаса товаров, т.е. условно говоря, определяет количество денег, которое он может истратить на покупку другого товара. Далее каждый к-й торговец выбирает при этих ценах и своих деньгах желаемый вектор потребления x и сообщает свое решение некоторому гипотетическому "секретарю рынка". Этот "секретарь" вычисляет общий спрос, а также общее предложение на рынке. Если общий спрос и предложение совпадают, то "секретарь" указывает на это совпадение участникам рынка, и они производят обмен своими товарами по принятым ценам. Конечно, вероятность такого совпадения очень мала, чаще всего общий спрос и предложение не совпадают: каких-то товаров надо больше, а других меньше. Поэтому "секретарь" подымает цены на товары, которых мало, и опускает цены на товары, которых много, затем сообщает свое решение участникам рынка. Торговцы снова пересчитывают свой товар уже в новых, предложенных "секретарем" ценах, и снова сообщают новый вектор потребления. Этот процесс продолжается до тех пор, пока спрос не совпадет с предложением. В этот момент цены устанавливаются равновесными, происходит обмен.
Термин "секретарь рынка" придумал Х.Удзава. С точки зрения теории управления "секретарь рынка" является алгебраическим сумматором, замыкающим рынок обратной связью и вырабатывающим сигнал ошибки.
Математическая постановка задачи
Так как цены не постоянны, то, строго говоря, вектор цен необходимо записывать как функцию времени p = p(t). Кривая изменения цен во времени является решением некоторого дифференциального уравнения. Для определения этого уравнения рассмотрим рынок с m-штук торговцами и n-штук товарами. При открытии рынка каждый продавец владеет своим вектором yk, причем эта величина остается постоянной и не меняется до установления равновесной цены, т.е. до обмена товарами.
Первое условие модели, которое должно выполняться: стоимость желаемых товаров для каждого продавца равна стоимости имеющихся товаров, т.е.
![]() для k=1,2,3,...m.
(1)
для k=1,2,3,...m.
(1)
Каждый участник рынка имеет свою функцию полезности ![]() .
.
Обратим внимание, что
вектор ![]() можно
рассматривать как вектор производства, а произведение
можно
рассматривать как вектор производства, а произведение ![]() может
трактоваться как доход потребителя:
может
трактоваться как доход потребителя: ![]() и уравнение (1) может быть записано как бюджетные
ограничения :
и уравнение (1) может быть записано как бюджетные
ограничения : ![]() .
Тем самым объединяются теория потребления и производства в одной модели, только
вектор x называется обычно вектором спроса, а вектор y -
вектором предложения.
.
Тем самым объединяются теория потребления и производства в одной модели, только
вектор x называется обычно вектором спроса, а вектор y -
вектором предложения.
Рассмотрим механизм формирования цен. Для этого введем вектор избыточного спроса рынка:
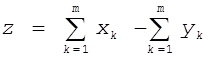 (2)
(2)
Мерность вектора z равняется
количеству разных типов товаров, предлагаемых к обмену на рынке, т.е. n.
Если какая-то координата вектора ![]() , то спрос на
, то спрос на ![]() превышает предложение
превышает предложение ![]() , если
, если ![]() , - то наоборот.
, - то наоборот.
Простейшее возможное предложение о характере изменения цен следующее:
скорость изменения цен пропорциональна избыточному спросу или просторавна избыточному спросу
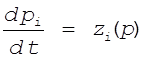 , i =1,2,..n (3)
, i =1,2,..n (3)
Часто система уравнений (3) записывается в векторной форме
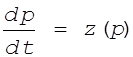 (3`)
(3`)
Кроме того, сделаем несколько предположений о функции z = z(p). Предположим, что z(p) - непрерывная функция p . (4)
Условие (4) вытекает из непрерывности функции полезности S(x). В противном случае не существовало бы прозводной в уравнениях (3).
![]() (5)
(5)
и если ![]() , то
, то ![]() (6)
(6)
Условие (5) отмечает
тот факт, что умножение цены на некоторую константу с=Const все равно
оставляет за этим числом понятие цены. Цена относительна, важно лишь
соотношение цен. Например, пусть 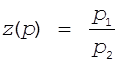 , тогда
, тогда 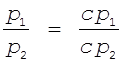 и можно записать, что
и можно записать, что ![]() .
.
Условие (6) означает, что если цена какого-то товара равна 0, то спрос на него все равно будет выше предложения.
Теперь необходимо определить, как будут изменяться цены, если выполняются принятые предложения (1) - (6).
Определение. Равновесной
ценой или равновесным вектором цен называется такой вектор ![]() , при
котором вектор избыточного спроса равен нулю. Действительно, если выполняется
условие равновесия цен
, при
котором вектор избыточного спроса равен нулю. Действительно, если выполняется
условие равновесия цен 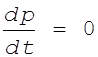 , то из (3`) следует, что
, то из (3`) следует, что ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.